2023. 12. 21. 14:50ㆍ알고리즘/문제풀이
1915번: 가장 큰 정사각형
첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 n개의 줄에는 m개의 숫자로 배열이 주어진다.
www.acmicpc.net

가장 먼저 떠오른 풀이는 백트래킹으로 모든 점을 탐색하면서 해당 점에서 한 변의 길이가 k인 정사각형을 만들 수 있는지 체크하는 풀이였다. 시간복잡도가 O(n^2 * m^2)이라 시간초과가 뜰 것 같아서 일단 패스했다. 시간초과를 생각해 보면 O(nm)으로 풀어야 한다. 즉, 한 번의 테이블 순회로 정사각형의 크기를 알아낼 수 있어야 한다는 뜻이다.
굉장히 규칙을 찾기가 힘들어서 테이블 순회는 어차피 열이나 행을 한줄씩 쭉 읽는 방식으로 작동하기에 한 번 손으로 순회하면서 어떻게 하면 한 번에 정사각형을 찾을 수 있을지 생각해 봤다.
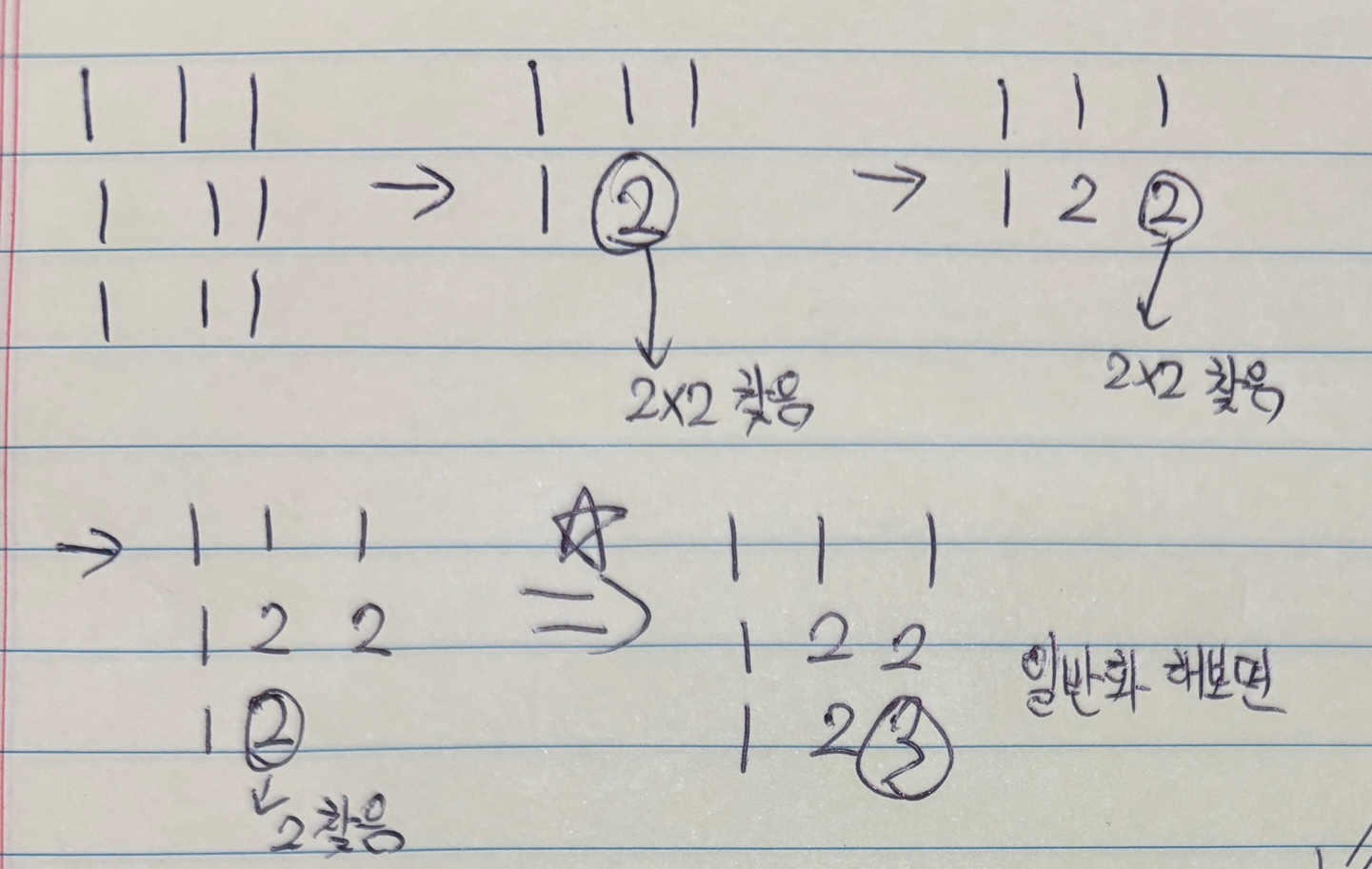
이런 식으로 2*2 정사각형과 3*3 정사각형을 발견할 수 있는 특정 시점을 찾았는데, 이를 일반화해 보자. 어떤 점 (x, y)를 기준으로 위, 왼쪽, 왼쪽 위 대각선에 길이 k인 정사각형이 있다면 (x, y)는 k+1의 정사각형의 한 점이라는 사실을 알 수 있다.

여기서 dp[i][j] = min({dp[i][j-1], dp[i-1][j], dp[i-1][j-1]}) + 1의 점화식을 찾을 수 있었고 구현은 쉽다.
사실 처음 문제를 풀면서 점화식을 찾는 건 실패했고 결국 다른 사람의 풀이를 참고해서 점화식을 찾았다. 다음에 비슷한 문제를 만난다면 이 글의 생각 흐름대로 점화식을 찾을 수 있을 것 같다. dp는 풀면 풀수록 어려운 것 같다.
/** DP 1915 가장 큰 정사각형 **/
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
int n, m;
int dp[1030][1030];
int board[1030][1030];
int ans = 0;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> n;
cin >> m;
for (int i = 1; i <= n; i++)
{
string str;
cin >> str;
for (int j = 1; j <= m; j++)
board[i][j] = str[j - 1] - '0';
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (board[i][j])
{
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
ans = max(ans, dp[i][j]);
}
}
}
cout << ans * ans << '\n';
}'알고리즘 > 문제풀이' 카테고리의 다른 글
| [BOJ] C++ 9655: 돌 게임 - 쉬운 DP문제 (1) | 2023.12.28 |
|---|---|
| [BOJ] C++ 10942: 팰린드롬? - 테이블 채우는 순서를 주의하자! (1) | 2023.12.26 |
| [BOJ] C++ 9084: 동전 - DP의 핵심은 중복 제거! (1) | 2023.12.20 |
| [BOJ] C++ 10844 쉬운 계단 수 - DP 테이블링 연습하기 (1) | 2023.12.18 |
| [BOJ] C++ 15486: 퇴사 2 - 테이블링이 어려운 DP (2) | 2023.12.18 |