[백준] 20955번: 민서의 응급 수술 - 그래프를 트리로 바꾸기
2024. 7. 9. 16:01ㆍ알고리즘/문제풀이
https://www.acmicpc.net/problem/20955
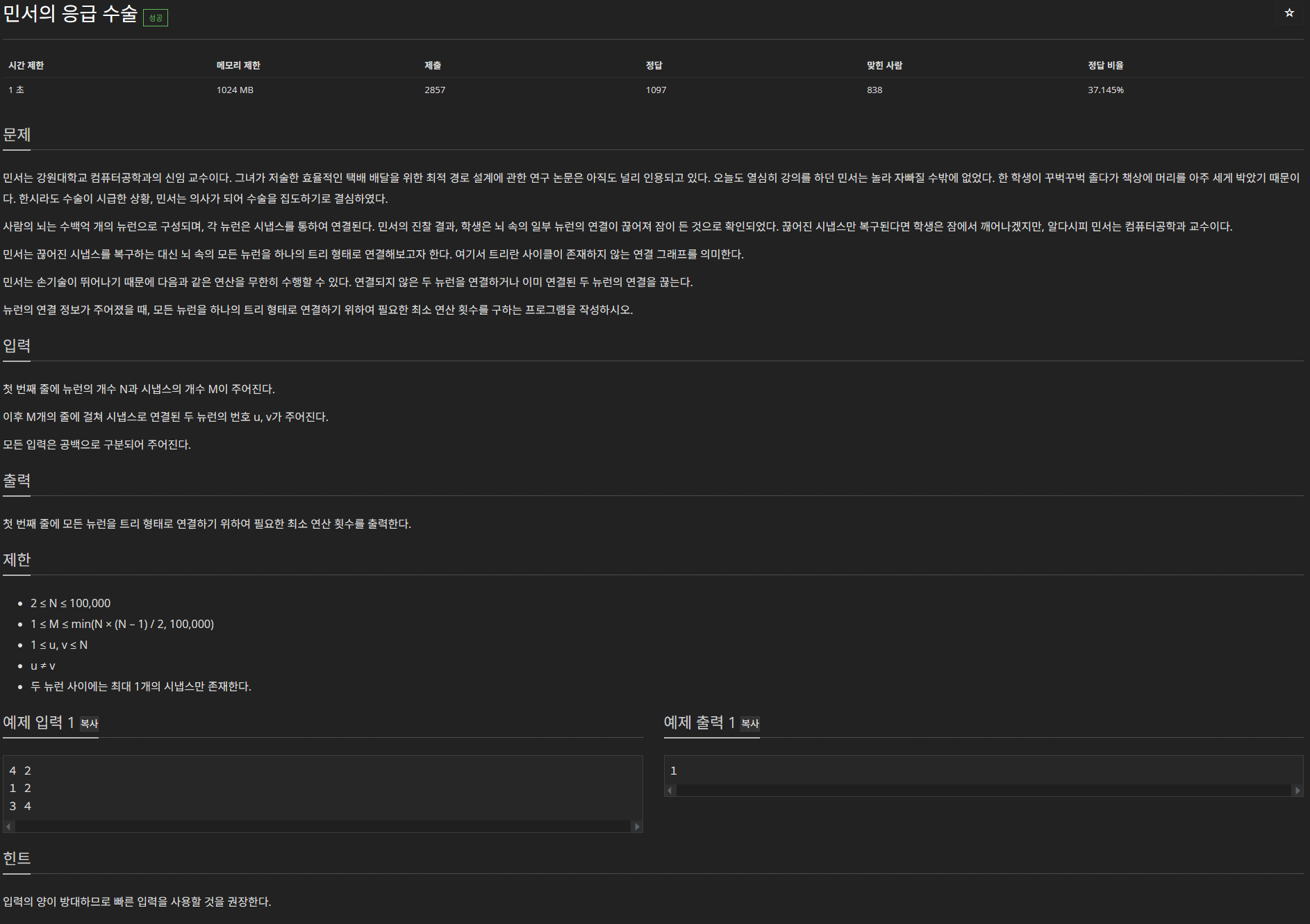
그래프를 트리로 바꾸면 된다. 이때 사용할 수 있는 특성은 트리는 n개의 노드에 대해 n-1개의 간선을 가지며 사이클이 없는 연결 그래프이다.
처음 떠올린 풀이는 우선, 연결 요소들을 파악해서 sub graph로 나누고, 그 그래프를 트리로 만든 뒤 그래프끼리 잇는 간선을 추가하는 풀이였다. 그런데 문제를 보면 N, M이 굉장히 크다. 따라서 sub graph를 트리로 만드는 과정을 시뮬레이션 방식으로는 절대 불가능하다고 판단하고 연산 횟수만 구하면 된다는 점에 집중했다.
우리는 어떤 간선을 제거할지는 생각할 필요가 없고, 적절한 간선을 선택했다고 가정하고 제거하는 횟수만 구하면 된다. 그렇다면 그 횟수는 어떻게 구할 수 있을까?
일단, sub graph끼리 연결하는 횟수는 graph의 수를 graph_count라 했을 때 graph_count - 1개의 간선을 생성하면 된다. 그렇다면 총 graph_count - 1 + m개의 간선이 존재할 텐데, n-1개의 간선만 존재해야 하므로 graph_count - 1 + m - (n-1)번의 제거 연산을 수행하면 끝이다!
/** Tree 20955 민서의 응급 수술 **/
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
vector<int> adj[100100];
bool vis[100100];
int n, m;
void dfs(int cur)
{
if (vis[cur])
return;
vis[cur] = true;
for (auto next : adj[cur])
dfs(next);
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
int graph_count = 0;
for (int i = 1; i <= n; i++)
{
if (vis[i])
continue;
dfs(i);
graph_count++;
}
// graph_count개의 그래프가 있음. 각 그래프를 연결하는 연산 graph_count-1번 수행
int ans = graph_count - 1;
// 각 그래프를 트리로 만들기 위해 간선 제거 연산 수행
// 어떤 간선을 제거할지는 몰라도 되고 몇 번 수행하는지만 알면 됨
// 현재 간선이 graph_count-1 + m개 있는데, 트리가 되려면 총 n-1개의 간선만 존재해야 함.
// 따라서 graph_count-1 + m - n-1 번의 제거 연산 수행
ans += m + graph_count - 1;
ans -= n - 1;
cout << ans;
}'알고리즘 > 문제풀이' 카테고리의 다른 글
| [백준] 21276번: 계보 복원가 호석 - 위상 정렬의 개념만 사용하기 (0) | 2024.07.17 |
|---|---|
| [백준] 2250번: 트리의 높이와 너비 - inorder 탐색, 루트 노드 찾기 (0) | 2024.07.14 |
| [백준] 4803번: 트리 - 무방향 그래프에서 DFS로 사이클 찾기 (0) | 2024.07.02 |
| [백준] 1707번: 이분 그래프 C++ - BFS, 큐를 사용하여 이분 그래프 판단하기. (0) | 2024.06.28 |
| [BOJ] C++ 3758: KCPC - 정렬 기준 설정하기 (1) | 2024.02.27 |