[백준] 21276번: 계보 복원가 호석 - 위상 정렬의 개념만 사용하기
2024. 7. 17. 15:51ㆍ알고리즘/문제풀이
https://www.acmicpc.net/problem/21276
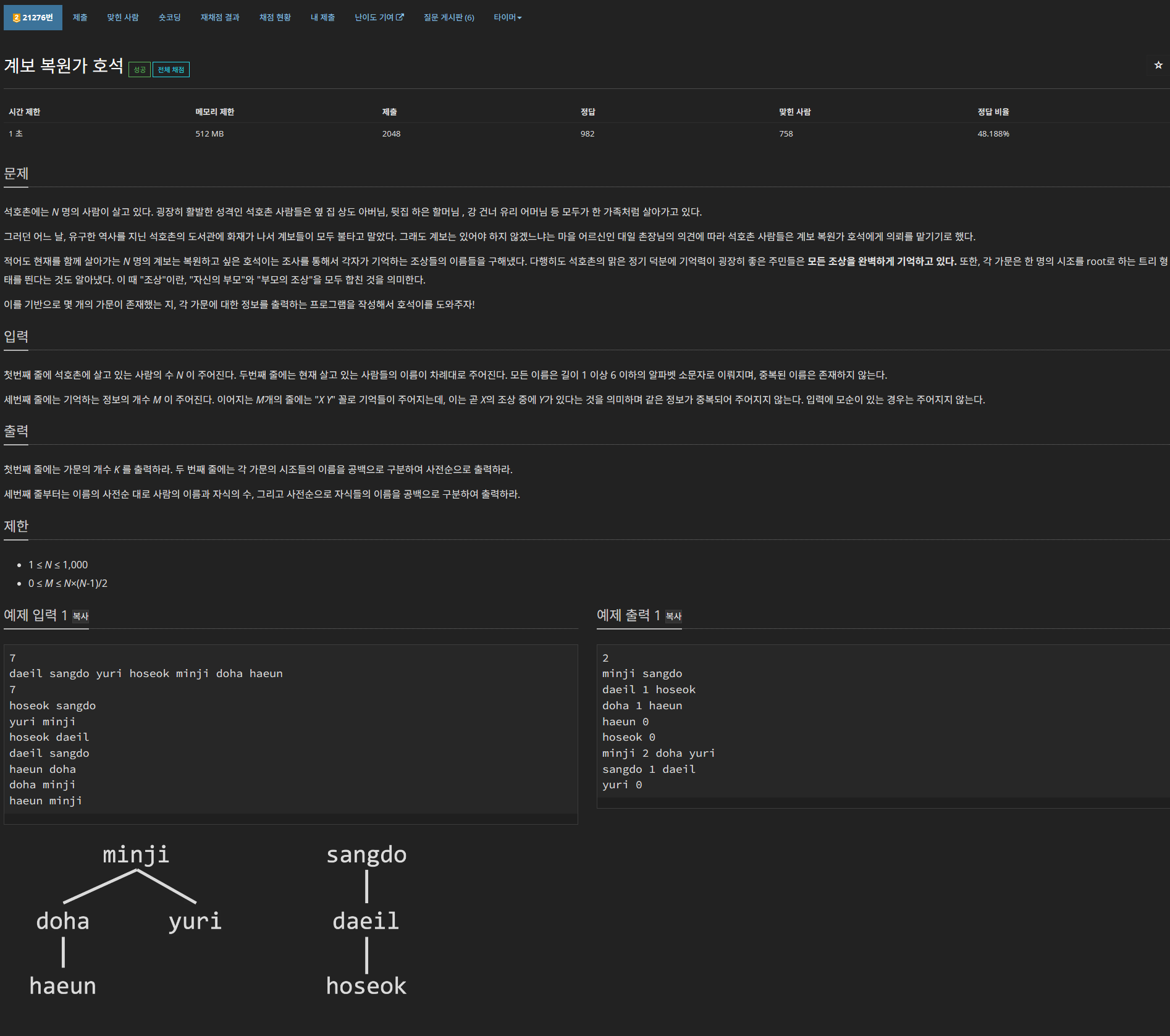
문제를 보고 떠올린 방법은 다음과 같다.
- indegree를 측정하는데, 편하게 측정하기 위해 string -> int로 index를 가지고 있는 map list를 생성하였다.
- indegree가 0인 노드가 가문의 시조가 되고, 위상 정렬을 하면서 사전순으로 방문해야 한다.
- 위상 정렬을 하면서 하나 방문하고 직계 자식을 구해야 하는데, 직계 자식은 indegree가 1이어야 한다. 즉, 현재 노드와 현재 노드와 연결된 간선을 제거했을 때 indegree가 0인 노드가 직계 자식이다.
이 정도로 알고리즘을 생각해 두고 구현해 봤는데 정렬을 하면서 직계 자식을 구하고, 위상 정렬을 수행하고 하는 과정이 너무 번거롭고 시간 복잡도 상으로 비효율적이었다.
그러다가 3번 풀이에서 떠올린 방법이 실제로 노드와 간선을 제거하는 방식이 아니라, 인접한 노드 중 indegree가 1 큰 노드가 직계 자식이라는 특징을 이용해 위상 정렬을 실제로 수행하지는 않고 indegree만 이용하는 방법이다.
알고리즘을 조금 구체화해보면 adj에 인접한 노드를 쫙 저장해 놓는다. adj는 vector 배열인데, adj의 index 또한 사전순으로 정렬되어 있다. 그리고 i번 노드에 대해 직계 자식을 저장하는데, 인접한 노드 중 indegree가 i번 노드보다 1만큼 큰 노드가 직계 자식이 된다. 직계 자식을 다 저장해 놓고 정렬하면 사전순으로 저장된다.
이걸 출력하면 끝이다! 실제로 위상 정렬을 구현하면서 로직을 짜면 굉장히 정렬이 힘들어지고 복잡해지지만 indegree로 자식을 찾아내는 개념만 가져오면 상당히 쉬워진다.
/** 위상 정렬 21276 계보 복원가 호석 **/
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <queue>
#include <map>
using namespace std;
int n, m;
string name[1002];
// 고유번호에 해당하는 name 찾기 : name string 배열 사용
int degree[1050];
vector<int> adj[1050];
map<string, int> list;
// name에 해당하는 고유번호 찾기 map 사용
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
cin >> name[i];
sort(name + 1, name + n + 1);
for (int i = 1; i <= n; i++)
list[name[i]] = i;
cin >> m;
for (int i = 0; i < m; i++)
{
string a, b;
cin >> a >> b;
adj[list[b]].push_back(list[a]);
degree[list[a]]++;
}
vector<int> k;
for (int i = 1; i <= n; i++)
{
if (degree[i] == 0)
{
k.push_back(i);
}
}
cout << k.size() << '\n';
for (auto x : k)
cout << name[x] << ' ';
cout << '\n';
// 트리에 존재하는 모든 사람에 대해 직계 자식을 출력하면 되는데, 직계 자식과 indegree 차이는 1이다.
// 또, 직계 자식들 또한 사전순으로 출력해야하기에 1번부터 adj를 정렬해야 한다.
vector<int> child[1050];
for (int i = 1; i <= n; i++)
{
// i번 노드에 대해 직계 자식을 구하기
for (int child_index : adj[i])
{
if (degree[child_index] == degree[i] + 1)
child[i].push_back(child_index);
}
sort(child[i].begin(), child[i].end());
}
for (int i = 1; i <= n; i++)
{
cout << name[i] << ' ' << child[i].size() << ' ';
for (int x : child[i])
cout << name[x] << ' ';
cout << '\n';
}
}
'알고리즘 > 문제풀이' 카테고리의 다른 글
| [백준] C++ 1368번: 물대기 - MST 변형, 프림 알고리즘 (0) | 2024.09.12 |
|---|---|
| [백준] 2637: 장난감 조립 - 왜 위상정렬인가? (0) | 2024.09.04 |
| [백준] 2250번: 트리의 높이와 너비 - inorder 탐색, 루트 노드 찾기 (0) | 2024.07.14 |
| [백준] 20955번: 민서의 응급 수술 - 그래프를 트리로 바꾸기 (0) | 2024.07.09 |
| [백준] 4803번: 트리 - 무방향 그래프에서 DFS로 사이클 찾기 (0) | 2024.07.02 |