2024. 10. 3. 08:00ㆍAI/CS231n
https://www.youtube.com/watch?v=vT1JzLTH4G4&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=3
스탠포드 대학교의 유명한 컴퓨터 비전 강의를 보고 정리한 글입니다.
https://www.youtube.com/playlist?list=PLetSlH8YjIfXMONyPC1t3uuDlc1Mc5F1A
CS231n 강의와 서울대학교 DSBA 연구실의 강의를 참고하여 공부한 부분을 정리하였습니다.
이번 강의를 들으면서 처음 AI 공부를 시작했고, 그만큼 틀린 부분 해석이 모호한 부분이 있을 수 있습니다.
4. NeuralNetwork, Backpropagation
1. Backpropagation Neural Network
Backpropagation
- 역전파로, 어떤 함수의 gradient를 계산하는 방식이다.
- chain rule을 재귀적으로 적용하는 방식이다.
- chain rule은 미분법의 중요한 성질 중 하나이고, 이를 재귀적으로 적용한다는 의미이다.
- 방식이 computational 하다는 특징이 있다.
- 신경망의 모든 연산 과정이 숫자로 표현되며, 이를 통해 계산이 가능하다는 뜻이다.
Backpropagation을 사용해서 gradient를 계산하는 이유는 다음과 같다.
- 파라미터를 update 할 수 있다.
- 부수적으로는 학습한 neural net을 시각화하는데 사용할 수 있다.
Neural Net은 결국 하나의 함수이다. 어떤 입력 data을 정의역으로 하여 neural net 함수를 거치면서 classification 문제라면 클래스라는 공역에 대응되게 되는 것이다.
neural net 함수는 여러 개의 hidden layers로 이루어져 있고 하나 하나의 layer가 parametric form, 즉 정해진 형식을 가진 함수가 된다. 따라서 neural net은 합성이 많이 된 함수 형태가 된다.
Chain Rule
- Chain Rule은 다음과 같은 합성 함수를 미분할 때 사용한다.위의 함수 z를 x에 대해 미분하려면 chain rule을 사용하여 다음과 같이 계산한다.
- $$ \frac {dz} {dx} = \frac {dz} {dy} ⋅ \frac {dy} {dx} $$
- $$ z = f(y), y=g(x)\to z=f(g(x)) $$
- 신경망에서는 입력부터 출력까지 여러 층이 쌓인 함성 함수로 이루어져 있다. Backpropagation은 loss를 기반으로 가중치를 조정하기 위해 각 가중치에 대한 손실 함수의 gradient를 계산하는 과정이다.
- backpropagation에서는 cahin rule을 사용하여 각 층의 가중치에 대한 gradient(미분값)을 구한다.
- chain rule이 중요한 이유는 신경망에서 각 층은 이전 층의 출력을 입력으로 받아들이기에, 각 층의 gradient는 이전 층의 gradient를 포함해야 한다. 따라서 손실 함수의 gradient를 계산할 때 cahin rule이 재귀적으로 적용되는 것이다.
Chain Rule exercise, Computational graph

$$ f(x, y, x) = (x+y)z $$
위의 식을 Backpropagation 방식으로 이해하기 위해 Computational graph를 사용하였다. x, y, z와 같은 symbol로 표현하는 것이 아니라 수치적으로 표현하게 되고 실제 컴퓨터에서 backpropagation을 계산하는 방식과 유사하다.
f를 z, x, y에 대해 미분한 값은 어떻게 구할 수 있을까?
$$ \frac {\delta f} {\delta z}, \frac {\delta f} {\delta x}, \frac {\delta f} {\delta y} $$
먼저 $f(-2, -5, -4) = -12$가 된다.
그리고 그래프의 빨간색 글씨는 각 항에 대한 gradient가 되는데 이를 계산할 때 chain rule이 사용된다.
계산 과정을 자세히 알아보자.
$$ \frac {\delta f} {\delta z} = \frac {\delta f} {\delta q}.\frac {\delta q} {\delta x} $$
위의 식이 chain rule의 기본이다. chain rule은 operator마다 단계별로 독립적으로 계산할 수 있다. 다만 주의할 점은 계산 할때와는 역순으로 계산해야 한다는 점이다.
$$ f(x, y, x) = (x+y)z $$
f에 대해 chain rule을 보면, f는 +, * operator를 가지고 있다. 계산의 역순으로 chain rule을 적용해야 하므로 *부터 계산해보자.
$x+y=q$라 하자. 그럼 $f(x, y, z) = qz$가 된다. f를 q로 미분한 값을 구하기 위한 식은 아래와 같다.
$$ \frac {\delta f} {\delta q} = \frac {\delta f} {\delta f}.\frac {\delta f} {\delta q} $$
따라서 f를 q에 대해 미분한 값은 z, f를 z에 대해 미분한 값은 q가 된다.

그래서 그래프의 값이 위와 같이 되는 것이다.
똑같은 방식으로 f를 x에 대해 미분하면 아래와 같은 수식이 된다.
$$ \frac {\delta f} {\delta x} = \frac {\delta f} {\delta q}.\frac {\delta q} {\delta x} $$
따라서 f를 q로 미분한 값은 -4이고, q를 x로 미분한 값은 1이 된다.
Local property of backpropagation
backpropagation에서 chain rule을 사용하다 보니 전체에 대해 미분하는 것은 어렵지만 각 operator별로 따로 미분하는 것은 쉬웠다.

위의 그림은 한 operator에 대해 gate만을 따로 도식화 한 것이다.
하나의 operator f에 대한 local gradient가 있다. 여기서 계산되는 결과 gradient는 이전에 계산한 gradient와 local gradient의 곱으로 표현된다.
그림을 예시로 설명하자면 다음과 같다.
- x, y는 input이고 f의 output은 z이다.
- y에 대해 전체 loss 함수를 미분한 값은 다음과 같다. $\frac {\delta L} {\delta y} = \frac {\delta L} {\delta z} . \frac {\delta z} {\delta y}$
- 여기서 $\frac {\delta z} {\delta y}$는 현재 gate의 local gradient이고 $\frac {\delta L} {\delta z}$가 이전(상단부) 게이트에서 전달된 gradient가 된다.
- 상단부 게이트부터 gradient를 계산하므로 역전파, backpropagation이 되는 것이다.
- 왜 재귀적으로 chain rule이 적용된다고 표현하냐면, 위에서 계산한 $\frac {\delta L} {\delta y}$는 y 아래 gate의 입장에서 위에서 흘러 들어온 gradient가 되고 똑같은 계산 방식을 거치면서 점점 뒤로 뿌려지게 되면서 끝까지 가면 말단에서의 gradient를 쉽게 계산할 수 있게 되기 때문이다.
이러한 이유에서 backpropagation을 gate 간의 communicating 라고 하는 것이다.
다른 예시도 보자.
$$ f(w, x) = \frac {1} {1+e^{-w^Tx}} = \frac {1} {1+e^{-w_0x_0+w_1x_1+w_2}} $$

6 종류의 gate에 대한 communication을 생각해보자. 위에서부터 아래로 gradient를 전달해주면 되므로 간단하다. 차례대로 계산해보자.
- $\frac {\delta f} {\delta f} = 1$ 이 $\frac 1 x$ 게이트로 흘러 들어온다.
- $\frac 1 x$ 게이트에서는 위에서 들어온 $1 * local\ gradient$ 가 된다. local gradient는 $\frac {\delta f} {\delta x} = -\frac {1} {x^2} = -\frac {1} {(1.37)^2} = -0.53$ 이다. 참고로 $\frac 1 x$ 게이트에서 말하는 x는 변수가 아니라 output이라 생각하면 된다.
- $+1$ 게이트에서는 $\frac {\delta f} {\delta x} = -0.53$ 이 흘러들어 온다. local gradient는 1이 된다.
- $exp$ 게이트에서는 -0.53 이 흘러 들어오고 local gradient는 $e^{-1}$이 되어서 -0.2가 된다.
- $*-1$ 게이트에서는 -0.2가 흘러 들어오고 곱하기이므로 local gradient가 -1이 되어서 0.2가 된다.
- $+$ 게이트는 상수 더하기이므로 local gradient가 1이 되어서 흘러들어온 값이 유지가 된다.
이런식으로 w0, x0, w1, x1, w2에 대한 gradient를 계산할 수 있었다.
다시 정리를 해보자면 일반 연산의 역순으로 backpropagation을 진행하면서 상단 게이트에서 흘러들어온 값과 local graident를 곱을 하단 게이트로 흘러보내게 되는 것이다.

Modularity
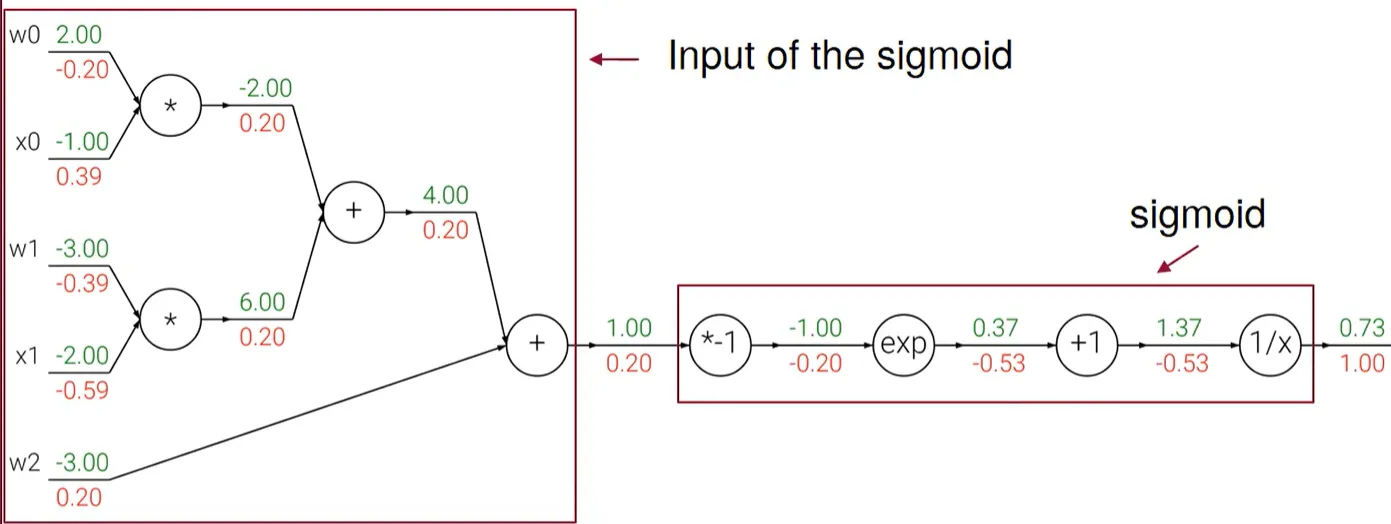
Back Propagation의 또 다른 장점으로 Modularity가 있다.
그림에서 왼쪽 부분을 sigmoid에 대한 input으로 보고, 오른쪽을 sigmoid 함수라고 생각할 수 있다는 특성이다.
이를 어떻게 활용할 수 있냐면 sigmoid function $\sigma (x) = \frac 1 {1+e^{-x}}$와 같이 정의할 수 있다.
sigmoid 를 미분하면 $\frac {\delta \sigma (x)} {\delta x} = (1-\sigma(x))\sigma(x)$가 된다.
sigmoid 함수에 대해 gate를 그려보면 다음과 같다.
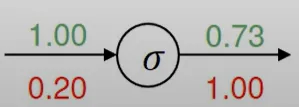
굉장히 간단해지는 것이다. local gradient를 x에 대해 계산하는 것이 아니고 $\sigma (x)$ 라는 것만 주의하자. 그래서 0.73을 쓰고 풀이가 다음과 같이 되는 것이다.
$$ (1-0.73)0.731=0.2 $$
예제에 나오진 않지만 max gate도 많이 나온다.
$f(x, y) = max(x, y)$
$$ \frac {\delta f} {\delta x} =1 (x \geq y), 0
$$
x가 더 크다면 x의 미분은 1, y의 미분은 0이 된다. 그래서 gradient router라고도 부른다.
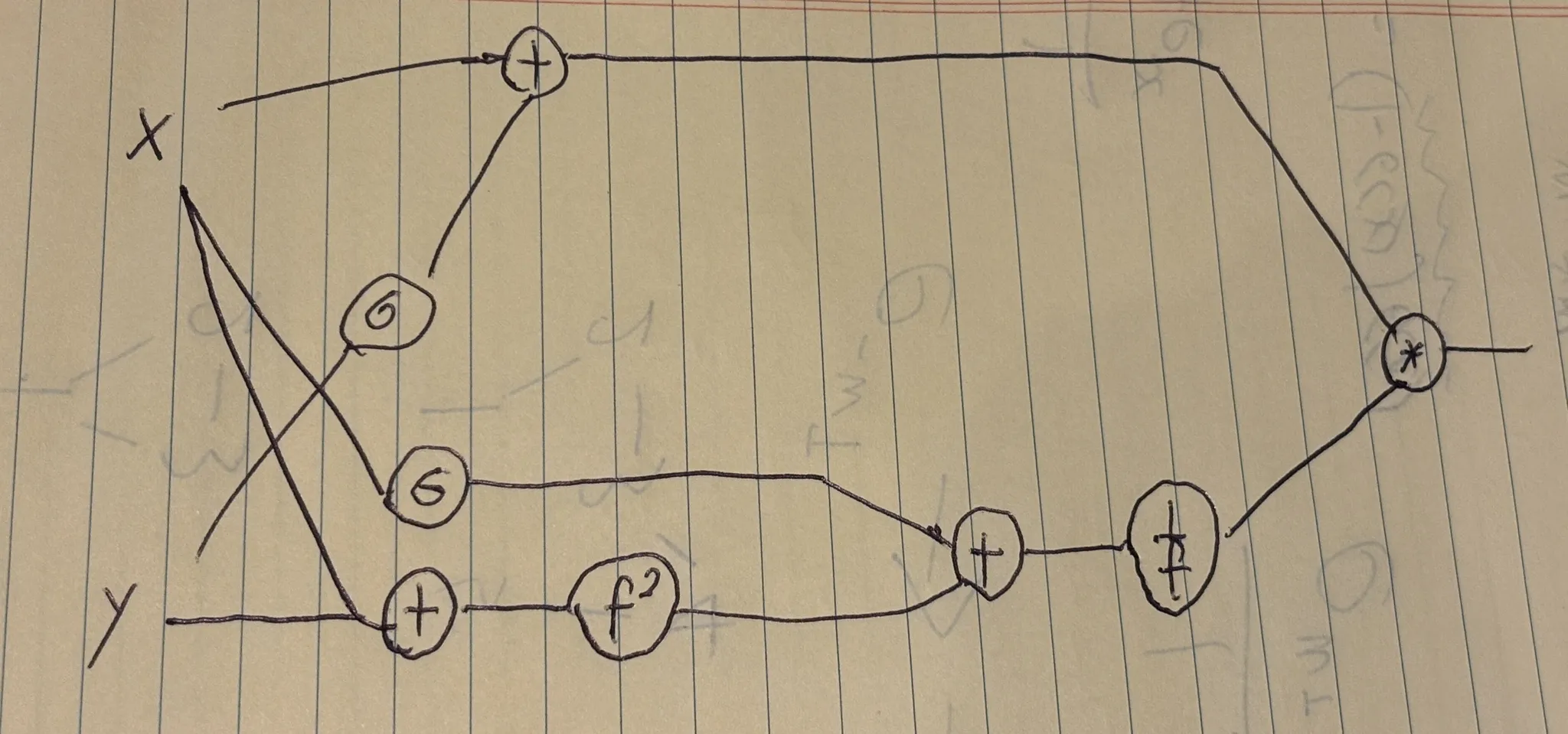
$$ f(x, y) = \frac {x+\sigma (y)} {\sigma(x) + (x+y)^2} $$
위의 함수에 대해 직접 computational graph를 그려보자.
계산의 순서대로 그려주면 된다.
2. Neural Network Resume
Parallel processing
병렬 처리에는 두 가지 패러다임이 존재한다.
Single Instruction Multiple Data (SIMD)
- 병렬 처리된 각각의 프로세스는 똑같은 명령을 수행하고 데이터만 쪼개서 다른 데이터를 처리하는 방식이다.
Multiple Instruction Multiple Data (MIMD)
- 여러 개의 프로세스가 다른 역할, 일을 하며 데이터도 쪼개서 다른 데이터를 처리하는 방식이다.
MIMD가 당연히 좋아보이지만 복잡도가 증가하고 SIMD는 간단하지만 할 수 있는 일이 적다. 그래서 그 사이에 있는 병렬 처리를 구현한 것이 Neural Network이다.
신경망에서는 각각의 뉴런이 하는 일이 정해져 있다. 미리 정해져있는 형태를 가지고 있는 것이지만 weight 값은 정해져있지는 않다. 똑같은 구조를 가지고 있음에도 weight 값에 따라서 각각의 뉴런들이 하는 일이 달라진다.
각각의 뉴런의 아키텍쳐가 같다는 면에서 SIMD와 유사하고 weight 값에 따라 하는 일이 달라진다는 면에서 MIMD와 유사하다.
즉, 역할을 각각의 유닛마다 프로세스에 따라서 분산시킨 것이다.
'AI > CS231n' 카테고리의 다른 글
| [DSBA] CS231n - 7. Convolutional Neural Networks (1) | 2024.11.10 |
|---|---|
| [CS231n] Training Neural Networks Part 1 (9) | 2024.10.09 |
| [CS231n] 3. Loss Function & Optimization (6) | 2024.09.26 |
| [CS231n] 이미지 분류의 pipeline과 K-NN based 이미지 분류, Cross Validation (3) | 2024.09.25 |