[CS231n] Training Neural Networks Part 1

[CS231n] Training Neural Networks Part 1

2024. 10. 9. 08:50ㆍAI/CS231n

https://www.youtube.com/watch?v=vT1JzLTH4G4&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=3

스탠포드 대학교의 유명한 컴퓨터 비전 강의를 보고 정리한 글입니다.

https://www.youtube.com/playlist?list=PLetSlH8YjIfXMONyPC1t3uuDlc1Mc5F1A

CS231n 강의와 서울대학교 DSBA 연구실의 강의를 참고하여 공부한 부분을 정리하였습니다.

이번 강의를 들으면서 처음 AI 공부를 시작했고, 그만큼 틀린 부분 해석이 모호한 부분이 있을 수 있습니다.

5. Training Neural Networks Part 1

1. Transfer learning

ImageNet data는 대략 1000개 클래스에 대해 어느정도 범용적인 이미지 data이다. 네트워크 자체에서 이미 학습된 weight를 초기 조건으로 사용하고우리가 학습시키고싶은 data로 fine tuning을 할 수 있다.

torch, tensorflow, mxnet, darknet 등등 유명한 모델들은 이런 weight를 구할 수 있다.

Transfer learning을 할 때 고려해야할 사항은 다음과 같다.

Pre train data와의 이질성
- Pre-train data과 이질성이 너무 크다면 transfer learning은 좋지 않을 수 있다.
Finetuning
분석의 할당된 시간
가용 가능한 hardware

2. Neural Network

신경망을 간단하게 알아보자.

Neural Network는 복잡한 데이터에서 패턴을 학습하고 이를 통해 예측하거나 분류하는 역할을 하는 인공지능 모델이다.

Layer

신경망은 여러 개의 layer로 구성된다. 각 layer는 입력을 받아 처리하고 다음 layer로 결과를 전달한다.

Input Layer : 이미지나 텍스트 등 실제 데이터를 입력받는다.
Hidden Layer : 입력 데이터를 처리하고 특징을 추출하는 역할을 한다. Hidden Layer를 Stacking 하는 것을 딥러닝이라 부른다.
Output Layer : 최종 예측 결과를 반환하는 층이다. 분류 task에서는 확률 값이나 클래스 레이블을 출력하고 회귀 문제에서는 역속적인 수치를 출력한다.

Weight

Weight는 신경망에서 각 뉴런과 뉴런 사이의 연결 강도를 나타내는 값이다. 입력 데이터가 각 layer를 통과할 때 각 입력은 weight와 곱해져 패턴을 학습하는데 핵심적인 역할을 한다.

각 입력은 그 중요성에 따라 다른 weight를 갖는다. 신경망은 학습을 통해 각 연결의 weight를 조정함으로써 최적의 예측을 할 수 있도록 한다.

Activation Function

신경망에서 각 뉴련의 출력값을 결정하는 함수를 Activation Function이라 한다. 주로 비선형성을 추가하는 역할을 한다. 신경망에서 layer를 stacking하는 과정에서 Activation 함수가 존재하지 않거나 함수가 선형 함수라면 여러 층을 stacking해도 결국 하나의 선형 변환과 다를 바가 없게 된다.

예를 들어 Activation Function이 $f(x) = ax$ 라면 3개의 layer를 거쳐도 결과가 $a^3x$가 되어서 stacking 하는 의미가 사라진다.

그래서 activation function은 비선형을 사용한다. tensorflow에서 대부분의 function을 제공하므로 사용하면 된다.

대표적인 Activation Function은 다음과 같다.

ReLU (Rectified Linear Unit) : 음수는 0으로, 양수는 그대로 통과시킨다.
Sigmoid : 출력값을 0과 1 사이로 압축하여 확률로 해석할 수 있게 해준다. 이진 분류 문제에서 많이 사용한다.
Tanh : 출력값을 -1과 1 사이로 변환한다.

Forward Propagation (순전파)

신경망이 주어진 입력을 처리하는 과정이다. 각 층에서 다음과 같은 절차로 연산이 이루어진다.

입력 데이터에 대해 각 입력값은 각 뉴런의 weight와 곱해지고 모든 뉴련의 가중합을 구한 후 bias를 더한다. $y = w_1x_1+w_2x+...+w_nx_n+b$
- bias는 weight와 입력값의 선형 조합에 상수값을 더하는 역할을 한다. 이는 Activation Function가 유연하게 동작하기 위함이다. bias 없이 모든 입력이 0일 때 Activation Function의 입력도 0이 된다. bias 또한 loss를 줄이는 방향으로 점차 조정된다.
가중치 합 y를 각 layer에서 설정된 Activation Function에 통과시켜 다음 layer로 전달할 비선형 변환된 값을 얻는다.
이 과정을 output layer까지 반복하여 최종 예측을 얻는다.
마지막 output layer에서 loss function을 통과하게 된다.

Backward Propagation (역전파)

Forward Propagation을 통해 예측을 한 후 실제 정답과 예측 결과 간의 loss를 계산한다. 이 loss를 기반으로 weight를 조정하게 된다.

역전파의 과정은 다음과 같다.

Loss Function : 신경망이 예측한 결과와 실제 값의 차이를 계산하는 함수로 이 값을 최소화하는 것이 학습의 목표이다. 예를 들어 분류 문제에서는 Cross-Entropy Loss를 사용하고 회귀 문제에서는 Mean Squared Error를 사용한다.
Gradient Descent : 손실 함수를 최소화하기 위해 weight를 조정하는 알고리즘이다. 각 손실 함수 $L$의 gradient를 weight $\omega$에 대해 계산하고 이를 기반으로 weight를 업데이트 한다.여기서 $\eta$는 학습률이며 기울기 반대 방향으로 weight를 업데이트하여 손실을 줄인다.
- $- \eta.\frac {\delta L} {\delta \omega}$ : 기울기 반대 방향으로 학습률만큼 weight를 이동한다. 학습률을 사용하는 이유는 weight를 너무 크게 이동시키면 손실 함수에서 최소점을 지나쳐 손실 함수 값이 더 커질 수 있고 너무 적게 이동시키면 학습이 매우 느리게 진행되기 때문이다.
- 기울기 반대 방향으로 움직이는 이유는 다음과 같다.
  - 기울기가 양수일 때 x를 증가시키면 Loss 값이 증가한다. 따라서 손실 함수를 최소화하기 위해서는 x를 줄여야 한다.
  - 기울기가 음수일 때 x를 감소시키면 Loss 값이 증가한다. 따라서 x를 증가시켜야 한다.
  - 즉, 기울기는 현재 위치에서 손실 함수가 증가하는 방향을 가리킨다.
- 사실 Gradient Descent는 직관적으로 이해하면 더 쉽다. 산을 오르내리는 상황과 정확히 일치하는데 산 정상이 손실 함수의 최대값이라 할 때, 현재 위치가 정상의 오른쪽에 있다면 정상을 기준으로 기울기는 왼쪽 방향을 가리킨다. 이때, 기울기 방향으로 이동하면 산을 오르게 되어 고도(손실)가 증가한다. 따라서 기울기 반대 방향을 이동하여 산을 내려오면 고도(손실)이 감소한다. 한 번에 얼마나 내리느냐가 learning_rate가 되는 것이고 수식이 $w = w - \eta.\frac {\delta L} {\delta w}$ 가 되는 것이다.
$\omega \leftarrow \omega - \eta.\frac {\delta L} {\delta \omega}$
Chain Rule : 역전파 과정에서 각 층의 weight에 대한 미분 값을 계산할 때 연쇄 법칙을 사용하여 이전 층부터 차례로 weight를 업데이트 한다. 즉, z가 activation function의 output이라 할 때 위에서 흘러들어온 $\frac {\delta L} {\delta z}$ * local gradient = $\frac {\delta L} {\delta x} = \frac {\delta L} {\delta z} . \frac {\delta z} {\delta x}$ 와 같은 수식으로 loss function에 대한 input 값의 미분을 계산할 수 있다.

3. Activation Function Family

Sigmoid

sigmoid 함수는 3가지 문제가 있다.

1. x값이 -5 ~ 5의 safe zone을 넘어가게 되면 gradient 값이 0에 수렴한다.

이를 Vanishing gradient problem 라 한다.

2. sigmoid output은 not zero-centered 이다. 만약 input 뉴련이 항상 양수라면 w 자체가 모두 양수가 되거나 음수가 된다. 그래서 zero mean data를 원하는 것이다.

3. ReLu는 max() 하나만 사용하지만 sigmoid는 exp() 연산을 해야하고 이 연산은 꽤나 비싸다.

Tanh

tanh 함수 또한 sigmoid 함수에서 2번 문제밖에 해결을 하지 못했다. 여전히 safe zone을 넘어가면 gradient가 특정 값에 수렴하고 exp() 연산을 사용한다.

ReLU

$f(x) = max(0, x)$

exp()를 사용하지 않고 max만 사용하기에 계산 효율이 상당히 좋다.
그러나 gradient가 음수일 때 0이고, 0일 때 원래는 계산할 수 없지만 float 단위로 계산하기에 소수점 단위까지 모두 0인 경우는 없다고 봐도 돼서 생각하지 않아도 된다.
여전히 Not zero-centered output이다.

Leaky ReLU

$f(x) = max(ax, x)$

여기서 a가 hyperparameter가 된다.

ELU

ReLU의 장점을 모두 가져 오고 gradient가 죽는 경우도 없고 output의 평균이 0에 수렴한다.
exp() 연산을 사용하므로 계산 속도가 느리다.

4. Weight

Weight Initalization

$w=a$

weight 값을 전부 0 혹은 상수로 둔다면 좋지 않다.

왜냐하면 Back Propagation에서 변화하는 양이 모두 같게 설정되기 때문이다. 자세히 알아보자.

뉴련 간 차별화가 없어진다. (Symmentry 문제)
- 신경망에서 각 뉴런의 weight는 독립적으로 학습되며, 각기 다른 특징을 학습해야 하지만 weight가 상수로 설정되면 각 뉴런은 동일한 입력에 대해 동일한 계산을 하게 된다. 따라서 각 뉴런의 출력 값이 동일하게 된다.
- 이때 역전파에서 모든 뉴런에 대한 기울기가 동일하게 계산된다.
기울기가 동일하면 학습의 의미가 사라진다.

5. Batch Normalization

CNN에서 defalut로 사용하는 알고리즘이다. 신경망의 학습 과정에서 학습 속도를 높이고 안정화시키기 위해 사용하는 기술이다. 신경망이 학습하는 동안 각 층의 출력을 정규화하여 학습이 더 잘 이루어지도록 돕고 기울기 소실 문제를 완화하고 학습 속도를 향상시킬 수 있다.

왜 Batch Normalization이 필요할까?

Internal Covariate Shift 문제를 해결하기 위해 도입되었다.

Internal Covariate Shift란 신경망의 각 층에서 입력 데이터의 분포가 학습 도중 계속 변화하는 현상을 말한다.

신경망은 학습 과정에서 weight를 업데이트하면서 각 층의 출력이 변화하게 되고 이후 층들에도 영향을 미친다.

그런데 특정 층에서 입력의 분포가 크게 변하면 그 다음 층에서는 변화된 분포에 맞춰 학습해야 한다. 이로 인해 학습 속도가 느려지고 모델이 수렴하기 어려워 진다.

Batch 단위로 training 할 때 만약 Layer 1에서 weight가 업데이트될 때 그 출력값의 분포가 크게 변했다면 Layer 2의 입력으로 이전 출력이 사용된다. 하지만 Layer 2는 이전 학습했던 입력 분포와는 다른 분포에서 데이터를 받게 되어 다시 학습해야 하고 이러한 변화는 연쇄적으로 모든 층에 영향을 미친다.

Batch Normalization의 목표는 각 층의 입력 분포가 너무 많이 변하지 않도록 보정하는 것이다. 동작 원리를 보자.

간단하게 말하자면 각 층에서 mini-batch 단위로 정규화를 수행한다. batch 단위로 입력값의 평균과 분산을 계산하여 이를 정규화한 후, 학습 가능한 매개변수 $\gamma$와 $\beta$를 사용하여 다시 스케일링하고 shift 한다.

자세히 알아보자.

각 Batch의 평균과 분산 계산 batch 내의 데이터 분포를 정규화하기 위해, 먼저 각 batch에서 입력 데이터의 평균과 분산을 계산한다.$$ \sigma ^2_B = \frac 1 m \sum^m_{i=1}(x_i-\mu_B)^2 $$$m$ : batch의 크기$\sigma ^2 _B$ : batch에 속한 데이터의 분산
$\mu_B$ : batch에 속한 데이터의 평균
$x_i$ : batch에 속한 입력 데이터 포인트
$$ \mu B = \frac 1 m \sum^m{i=1}x_i $$
정규화 입력 데이터에 평균을 빼고 분산으로 나누어 표준화한다. 입력 데이터를 평균이 0, 분산이 1이 되도록 조정하는 것이다.여기서 $\epsilon$은 수치적으로 0을 나누는 것을 방지하기 위한 작은 값이다.
$$ \hat x_i = \frac {x_i-\mu_B} {\sqrt {\sigma^2_B + \epsilon} } $$
스케일링과 이동(shifting)$$ y_i = \gamma \hat x_i + \beta $$$\beta$ : 이동 파라미터, 정규화된 값의 평균을 조절한다.
$\gamma$ : 스케일 조정 파라미터, 정규화된 값의 표준편차를 조절한다.
정규화된 값만으로는 모델이 너무 제한적일 수 있기에 각 정규화된 값을 hyperparameter $\gamma$, $\beta$로 스케일링하고 이동한다.

Batch Normalization을 통해 높은 학습률을 수용할 수 있고 initialization의 의존도를 낮출 수 있다.

예시를 보자.

gamma의 초기 값은 1, beta의 초기 값은 0으로 둬서 스케일링과 이동은 시키지 않는다.

코드로도 보자.

import numpy as np


def batchnorm_forward(x, gamma, beta, eps):
    # N = batch size, D = number of features
    N, D = x.shape

    #step1 : calculate mean
    mu = 1./N * np.sum(x, axis = 0)

    #step2 : subtract mena vector of every training example
    xmu = x - mu

    #step3 : following the lower branch - calculation denominator
    sq = xmu ** 2

    #step4 : calculate variance
    var = 1. * np.sum(sq, axis=0)

    #step5 : add eps for numerical stability, then sqrt
    sqrtvar = np.sqrt(var + eps)

    #step6 : invert sqrtwar
    ivar = 1./sqrtvar

    #step7 : execute normalization
    xhat = xmu * ivar

    #step8 : Nor the two transformation steps
    gammax = gamma * xhat

    #step9 : Shifting
    out = gammax + beta

    #store intermediate
    cache = (xhat, gamma, xmu, ivar, sqrtvar, var, eps)
    return out, cache

Back propagation의 코드도 보자.

def batchnorm_backward(dout, cache):
    # unfold the variables stored in cache
    xhat, gamma, xmu, ivar, sqrtvar, var, eps = cache

    # get the dimensions of the input/output
    N, D = dout.shape

    # step9
    dbeta = np.sum(dout, axis=0)
    dgammax = dout  # not necessary, but more understandable

    # step8
    dgamma = np.sum(dgammax * xhat, axis=0)
    dxhat = dgammax * gamma

    # step7
    divar = np.sum(dxhat * xmu, axis=0)
    dxmu1 = dxhat * ivar

    # step6
    dsqrtvar = -1. / (sqrtvar ** 2) * divar

    # step5
    dvar = 0.5 * 1. / np.sqrt(var + eps) * dsqrtvar

    # step4
    dsq = 1. / N * np.ones((N, D)) * dvar

    # step3
    dxmu2 = 2 * xmu * dsq

    # step2
    dx1 = (dxmu1 + dxmu2)
    dmu = -1 * np.sum(dxmu1 + dxmu2, axis=0)

    # step1
    dx2 = 1. / N * np.ones((N, D)) * dmu

    # step0
    dx = dx1 + dx2

    return dx, dgamma, dbeta

forward propagation을 계산하다보면 loss가 구해지게 되고, 다시 back-propagation을 계산하면서 local gradient를 구하게 된다.

역전파 과정을 자세히 알아보자.

step 9

Add gate는 gradient distributor 이므로 local gradient가 1이 된다. $d\beta$는 Batch 단위의 합을 의미하게 되니 합하면 된다.

step 8

mul gate는 gradient router이므로 반대로 보내주게 된다. Beta와 마찬가지로 변수당 하나의 gamma가 존재하므로 batch 수만큼 edge들을 합하면 각 변수의 gamma gradient가 계산된다.

step 7

step 8과 마찬가지로 Gate 기준 윗 부분은 각각의 gradient에 input의 반대방향을 곱하여서 바꾸어 준다. Gate 기준 밑부분은 Standard deviation(표준편차)을 나누기 위해 Batch 기준으로 합한다.

step 6

분수 미분꼴로 $-\frac 1 {input^2}$을 곱해주게 된다.

step 5

sqrt(f(x))의 미분꼴로 곱해주고 다시 전파한다.

step 4

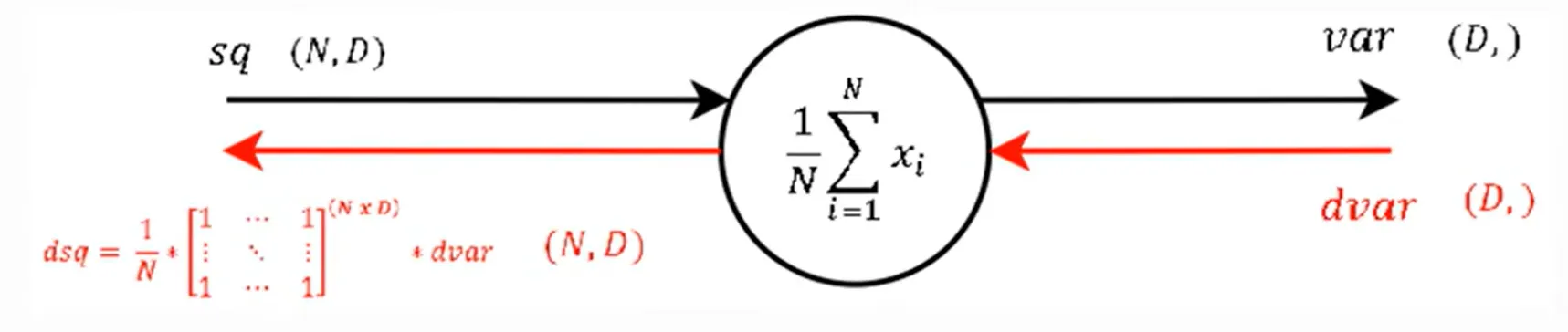
N은 Batch size 따라서 $\frac 1 N$은 constant mul gate와 같다. 그리고 $\sum^N_{i=1} x_i$ 부분은 step 9와 반대되는 개념으로 원래의 batch size대로 분배 해준다. 결국 Add gate에서 edge의 개수가 batch 수가 되기 때문이다.

평균 연산의 역전파는 배치 크기 N에 따라 기울기가 조정된다. 순전파에서 각 입력이 N으로 나눠졌기 때문에 역전파에서는 이 나눠진 비율을 다시 반영하여 기울기를 분배하는 것이다.

step 3

step 2

위에서 흘러 들어온 두 개의 gradient가 결국 합쳐지는 형태이기에 합쳐준다.

gate가 $x-\pi$이기 때문에 1과 -1이 local gradient가 되고 Sigma로 들어가는 Gate를 통과해야 하기에 Batch 단위 만큼 합하여 주었다.

step 1

step 0

정리해보자면 Batch Normalization을 사용하는 것을 보면 Input, Batch-Normalization, Activation Function으로 이루어져 있다.

6. Learning Process

1. Preprocess the data

2. Choose the architecture

네트워크의 아키텍쳐를 선택한다. hidden layer가 몇 개인지 등을 결정하는 과정이다.

네트워크를 선택했고 코드로 구현했다고 생각해보자.

regularization은 끄고 10개의 클래스에 대해 classification 문제에 대해 각각의 weight는 랜덤 값으로 줬을 때 loss 값이 초기값으로 잘 설정돼었는지 알아보자.

위의 코드는 score 값을 구하고 score 값에 대해 Soft Max를 구한 다음 loss in cross entropy를 구할텐데, 결국 weight를 random하게 줬으므로 score가 uniform하게 구해질 것이다. 여기서 나온 loss 값인 2.3026…은 10개의 클래스를 갖는 분류 문제에서의 초기 Cross Entropy Loss 값으로 네트워크 모델을 옳게 구현했다고 볼 수 있다.

무슨 뜻이냐면, 예측 확률이 모든 클래스에서 같다면 Cross Entropy Loss는 $-log(\frac 1 {10}) = log(10) = 2.3026...$ 과 같이 구해지므로 제대로 된 초기화 결과라는 것이다.

위의 코드처럼 regularization 값을 조금 주면 Loss 값이 좀 더 올라가야 한다. 참고로 여기서 말하는 정규화는 Batch Normalization이 아니고 L2 Regularization이다.

모델의 가중치가 너무 커지는 것을 방지하기 위한 기법으로 손실 함수에 가중치의 제곱합을 추가하는 방식이다. 식을 다시 보자.$\lambda$는 정규화 강도를 조절하는 하이퍼파라미터로 높을수록 더 강한 정규화가 이루어
$$ Loss = Cross-Entropy Loss + \lambda\sum W^2_i $$

hyperparameter 중 learning rate에 따라서 학습이 어떻게 진행되고, 어떤 경우에 어떤 learning rate를 사용해야하는지 알아보자.

learning rate를 굉장히 작게 잡고 10개의 class의 분류문제를 보면, 10번의 epoch를 돌았음에도 cost가 전혀 줄지 않고 있다. learning rate가 너무 낮은 것이다.

반대로 learning가 너무 큰 경우 cost가 nan이 나오는 것을 확인할 수 있다.

결과를 보면 알 수 있듯이 직관적으로, loss rate가 너무 줄어들지 않으면 learning rate가 너무 작은 것이고 cost가 폭발해버리면 learning rate가 너무 큰 것이다.

손실 함수 값이 폭발한다는 뜻은 가중치가 너무 큰 폭으로 업데이트되어 잘못된 방향으로 심하게 이동해서 손실 함수가 빠르게 커지거나 발산해버리는 것을 말한다.

7. Hyperparameter Optimization

최적화는 log space에서 하는게 더 좋다.

log space는 넓은 범위의 값을 효율적으로 탐색할 수 있고 작은 값과 큰 값 모두 균형 있게 탐색할 수 있기 때문이다.

hyperparameter를 최적화하기 위해 search를 하다 보면, 하나씩 좋은 값이 튈 수 있다. 그 경우 그 값이 제일 좋은게 아니라 그 뒤의 추세를 봐야 한다.

또, 추세 없이 딱 하나의 점에서 좋다면 일반화된 데이터에서 좋은 성능을 보이지 않을 수 있다.

극단적인 예시긴 하지만 Grid Layout 보다 Random Layout으로 search 하는게 더 좋을 수 있다.

강의에서 추천하는 hyperparameter search 방법은 아래와 같다.

learning rate는 loss 그래프를 보면서 판단
Activation Functions : ReLU
Data Processing : images : subtract mean
Weight Initalization : Xavier init
Batch Normalization : use
Hyperparameter Optimization은 random sample을 log space에서 탐색하기

저작자표시 비영리 변경금지

'AI > CS231n' 카테고리의 다른 글

[DSBA] CS231n - 7. Convolutional Neural Networks (1)	2024.11.10
[CS231n] 4. NeuralNetwork, Backpropagation (5)	2024.10.03
[CS231n] 3. Loss Function & Optimization (6)	2024.09.26
[CS231n] 이미지 분류의 pipeline과 K-NN based 이미지 분류, Cross Validation (3)	2024.09.25

조준화의 오류정정