2024. 12. 15. 20:47ㆍCS/Information Retrieval
정보검색의 꽃. 굉장히 중요한 부분이다!
이번 챕터의 Term frequency, Tf-idf ranking, Vector space model은 반드시 시험에 나오니 잘 익혀두자.
1. Ranked retrieval
기존에는 단어가 포함된 문서를 찾는 boolean retrieval을 다루었다. 그런데 어떤 단어는 많은 관련이 있고 어떤 단어는 등장하기만 할 수 있다. 중요도가 없는 것이다.
expert users, application에게는 boolean retrieval이 좋을 수 있다. 전문가는 &, |를 잘 설정해서 관련된 문서의 개수를 잘 조절할 수 있지만 일반 사용자들에게는 불가능하다.
예를 들어 변호사는 오래 걸리더라도 관련된 모든 정보를 다 봐야 하지만일반 사용자들은 1000개가 넘는 문서를 다 볼 수 없다.
또, boolean retrieval은 feast 하거나 famine하다.
예를 들어 [standard user dlink 650]을 boolean으로 검색했더니 200,00개의 결과가 나왔다. feast하다.
그래서 [standard user dlink 650 no card found]를 검색했더니 0개의 결과가 나왔다. famine하다.
ranking을 사용하면 가장 관련있는 10개의 결과만 보여주므로써 위의 문제를 해결할 수 있다.
ranking 알고리즘의 기본 전제는 더 관련있는 결과가 상위의 랭크를 받아야 한다는 것이다.
이를 위해서는 쿼리와 문서 사이의 점수를 매기는 것이 중요하고 점수는 [0, 1] 사이의 값으로 나타난다.
- 확률로 표현하기 위해 [0, 1] 사이로 정규화시키는 것이다.
점수는 document와 query가 얼마나 match되는지를 측정한 것이다.
document를 score로 sorting 해주면 ranking이 된다.
쉬운 예를 들어보자. 문서에 질의어 단어가 없다면 score는 0이 된다. 그리고 쿼리의 단어가 많이 나오면 score가 더 높아야 한다.
어떤 문서는 쿼리의 많은 단어가 나오고 어떤 문서는 쿼리의 한 단어가 많이 나온다면 쿼리의 많은 단어가 나오는 문서의 score가 더 높아야 한다.
이런 기준을 맞춰주면서 ranking을 매겨보자!
Take 1: Jaccard coeffcient
A, B라는 두 set가 있으면 Jaccard coeffceint는 다음과 같다.
$$ JACCARD(A, B) = \frac {|A \cap B|} {|A \cup B|} $$
JACCARD(A, A) = 1
if$(A\cap B = 0)$ JACCARD(A, B) = 0
따라서 JACCARD 값은 항상 0~1 사이로 나타난다.
예를 들어
- Query : “ides of March”
- Document: “Caesar died in March”
$q \cup d$ = 모든 단어 = 6
$q \cap d$ = 겹치는 단어 = 1
따라서 JACCARD(q, d) = 1/6
Jaccard의 문제점은 term frequency를 고려하지 않고 단어의 중요도 또한 고려하지 않는다는 것이다.
예를 들어 알츠하이머 병 쿼리에 대해 알츠하이머는 병보다 더 특수하므로 중요한 단어이다. 많이 나오지 않는 term은 많이 나오는 단어보다 더 중요한데 이를 고려하지 않는 것이다.
또, document의 길이 또한 고려하지 않는다.
이 세 가지를 고려하는 것이 중요하다.
2. Term frequency

term document incidence matrix를 생각해보면 단어가 문서에 존재하면 1이다. 2진수로 나타나게 된다. 따라서 document vector가 \{0, 1\} ^ {|V|}가 된다. V는 vocabulary size이다.

여기서 2진수 대신 term frequency를 적어주면 Count matrix가 된다. 여기서 document vector는 $N^{|V|}$가 된다. N은 정수를 나타낸다. vector가 정수의 vocab size의 차원으로 나타난다는 뜻이다.
Bag of words model
words의 순서를 고려하지 않는 모델을 bag of words Model이라 한다.
- John is quicker than Mary
- Mary is quicker than John
- 위의 두 문서는 Bag of words model에서 같은 문서로 취급된다.
postional index를 사용하면 두 문서를 구분할 수 있지만 일단 Bag of words model만 다뤄보자.
term frequency tf
term frequency는 tf로 약칭해서 많이 부른다.
document d에 term t가 몇 번 나타났는지를 표현하려면 $tf_{t, d}$로 표현한다.
이제 query-document match socres를 구할 때 tf를 사용하면 되는데, 어떤 문서에서 boy가 3번 나오고 어떤 문서에서 boy가 1번 나오는 상황에서 score를 3배로 세팅하면 안될 것 같다.
따라서 tf에 로그를 취해 다음의 수식을 사용한다.
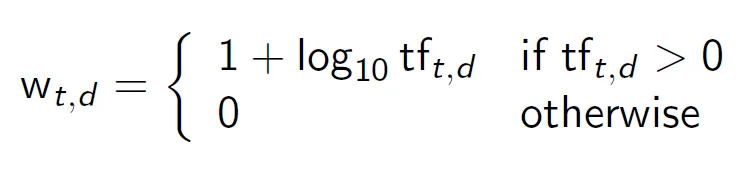
상용로그라는 점이 중요하다! 1을 더해준 이유는 tf가 1일 때 값이 0이 되는 것을 막아주기 위함이다. tf가 1이라는 것은 문서에 term이 한 번 등장한다는 것인데 score가 0이 되어서는 안된다.
- tf → w를 계산해보자. 0 → 0, 1 → 1, 10 → 2, 1000 → 4, …
쿼리에서 나온 term과 document에서 나온 term의 frequency를 만들고 교집합을 구해서 다 더해주면

이렇게 된다. 여기서 주의할 점은 tf를 쿼리에 대해서가 아니라 document에 대해서를 구해야 한다는 것이다. 또 t가 q \cap d의 원소이기에 최소한 한 번 나온 t이다.
3. tf-idf weighting
문서의 집합 collection에서 term이 얼마나 나왔는지를 collection frequency라 한다.
이 collection frequency를 이용하면 score를 좀 더 잘 구할 수 있다.
예를 들어 알츠하이머 병이라는 쿼리에 대해 알츠하이머가 더 중요한데 이를 어떻게 객관적으로 측정할 수 있을까?
전체 collection에서 Rare terms가 frequent terms보다 more informative하다.
즉, 전체 집합에서 더 적게 나온 단어가 더 중요하다. tf와는 반대이다!
idf weight
$df_t$는 term t가 등장한 document의 수로 document frequency이다. $df_t$가 클수록 t는 덜 중요하다. 따라서 idf는 다음과 같이 정의할 수 있다.
$idf_t = log_{10} \frac N {df_t}$, N은 collection의 문서의 수이다.
$idf_t$는 term이 얼마나 중요한지를 나타내고 N에 log를 씌워서 사용하기도 한다.

위의 예시를 생각해보면 N을 10^6이라 했을 때 idf를 계산할 수 있다.
ranking에서 idf의 영향을 생각해보자.
- idf는 2개 이상의 term을 갖는 쿼리에 대해 영향을 준다.
- 예를 들어 arachnocentric line 쿼리에 대해 상대적으로 ARCHNOCENTRIC은 idf가 커지고 LINE은 작아질 것이다.
- idf는 단일 term 쿼리에는 영향을 미치지 못한다.
Collection frequency VS Document frequency

Collection frequency : 전체 collection에서 해당 term이 등장한 총 횟수
Document frequency : 해당 term이 등장한 문서의 수
참고로 term frequency는 해당 term이 문서에서 몇 번 등장했는지이다.
어떤 단어가 더 좋은 search term일까?
INSURANCE가 더 중요한 단어이다.
- 두 term은 비슷한 cf를 갖지만 INSURANCE는 더 적은 수의 문서에서 등장한다. 따라서 INSURANCE가 특정 주제와 관련이 더 높은 중요한 단어이다.
이 예제는 df와 이를 바탕으로 한 idf가 cf보다 weighting에 좋다는 것을 보여준다.
tf-idf weighting
tf-idf는 tf * idf로 간단하게 나타내는 것이다.
$$ w_{t, d} = (1+logtf_{t, d}) . log\frac {N} {df_t} $$
term t, document d, N은 전체 문서의 개수가 되고, 1+log tf 가 tf, log N/df 가 idf이다.
tf-idf가 가장 잘 알려진 weighting scheme이다.
term frequency가 증가하면 weight가 증가한다.
collection에서 term의 희귀도가 증가하거나 inverse document frequency가 줄어들면 weight가 증가한다.

df와 cf의 관계는?
- 하나의 문서에서 단어가 여러 번 등장할 수 있기에 df ≤ cf 이다.
tf와 cf의 관계는?
- 모든 문서의 tf의 합은 cf와 같다.
tf와 df의 관계는?
- tf는 문서에서 term이 많이 등장할 수록 커진다면 df는 문서에서 term이 많이 등장하던 한 번 등장하던 1 씩 증가한다.
4. The vector space model
지금까지 term, document를 어떻게 표시했는지 생각해보자.

2진수

정수

실수
document를 vector로 나타내보자.
- 각 문서는 tf-idf weights 를 가지는 실수 벡터로 표현된다.
- $R^{|v|}$ = document vector가 v차원으로 나타난다는 뜻이다. v는 term의 수가 되고 document vector는 세로로 읽는다.
- 벡터 공간에서 term은 축이 되고 문서는 공간에서의 점 혹은 벡터가 된다.
- 정보 검색에서는 보통 50만개의 어휘를 다루기에 50만차원의 벡터를 다뤄야 한다.
- Very high-demensional이고 각 vector는 매우 sparse하다. 대부분이 zero를 가진다.
쿼리를 벡터로 나타내보자.
- Key idea 1 : 쿼리도 똑같이 벡터로 나타낸다.
- Key idea 2 : 쿼리와 문서 사이의 proximity를 계산해서 ranking에 이용한다.
- proximity는 similarity와 유사하고 distance와 반대가 되는 개념이다. 유사하다는 것은 거리가 멀다는 것이고 따라서 거리에 역수를 취하면 된다.
feast-or-famine Boolean model을 피하기 위해 rank를 사용하여 연관된 문서를 찾아주는 검색을 만들어보자!
정리하자면 모든 문서를 벡터 공간으로 매핑하고 질의어 또한 벡터 공간에 올려두고 가까운 정도를 가지고 유사도를 구하면 된다.
그렇다면 어떻게 유사도를 구할 수 있을까?
Euclidean distance
벡터 사이의 거리에 역수를 구한다.
그런데 Euclidean distance는 벡터의 각도와 관계 없이 끝의 point를 기준으로 거리를 구하기에 실제로는 굉장히 가까워도 멀다고 구해질 수 있다.
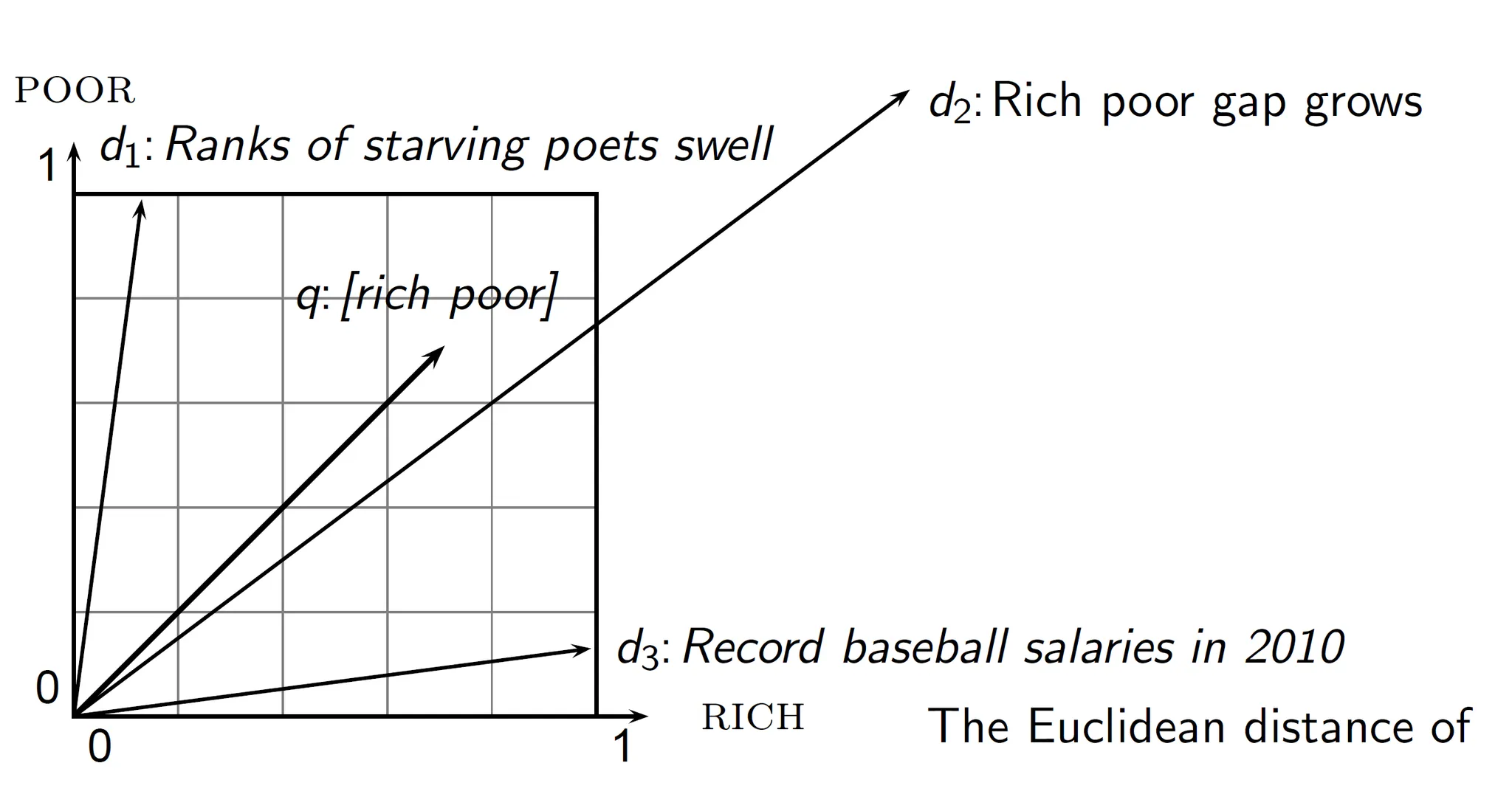
POOR, RICH 두 단어에 대해서만 벡터공간을 만들고 [rich poor] 질의가 들어온 상황이다.
실제로는 d2가 쿼리와 굉장히 가까운데 Euclidean distance는 d1과 더 가깝다. Euclidean distance는 벡터의 크기가 포함되기 때문이다.
Use angle instead of distance
문서 d1과 d1 두 개를 붙인 문서 d2를 생각해보자. 정확히 똑같은 term이 두 배 등장하므로 Euclidean distance는 두 배 증가하지만 사실 똑같다고 인식해야 한다.
따라서 각도를 사용해서 cos 값을 사용하여 유사도를 계산하는 방법이 좋다. 각도를 [0, 180] 도를 사용하면 실제 값은 -1 ~ 1이 나온다.
자세한 방법을 알아보자.
일단 길이가 1이 되게 normalization 한다.
벡터의 길이 = $L_2$ $L_2$ $L_2$$||x||^2 = \sqrt{\sum_ix^2_i}$
최종 식은 다음과 같다.

qi, di의 tf-idf weight를 값으로 주면 q와 d의 cosine 유사도를 구할 수 있다.
normalized vector에 대해서는 길이가 이미 1이므로 내적만 구해주면 된다.

다시 아까 [rich, poor]의 예시를 보자.

Cosine: Example

이 세가지 소설의 유사도를 구하기 위해 소설에 나오는 단어의 frequencies를 구해보았다.

log frequency = $log_{10}fi + 1$
cosine normalization
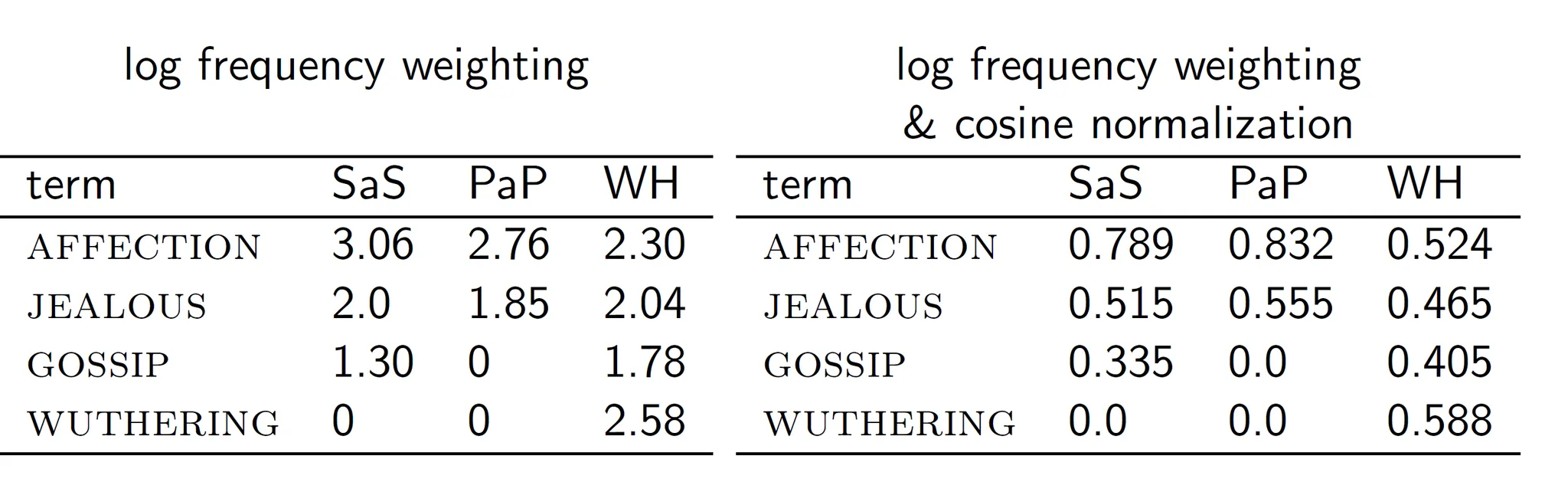
normalization이 됐으므로 각 문서의 내적을 구해서 유사도를 구해보면 cos(SaS, PaP) = 0.94 정도가 나온다. 한 번 계산해보자.
- 왜 cos(SaS, PaP)가 cos(SaS, WH)보다 클까?
- PaP가 0이 더 많고 WH가 더 유사해보이지만 PaP가 더 유사한 이유는 AFFECTION, JEALOUS의 값이 많이 나와서 값이 더 크기 때문이다.

inverted index를 사용하므로 코드상으로는 더 복잡하다.
query term t에 대해 weight를 계산하고 t에 대한 posting list를 가져온다.
원래 inverted index와 다르게 지금은 posting list에 docID, tf(t, d) pair로 달아둬야 한다.
d, tf(t, d) pair를 posting list에서 가져와서 score를 계산해준다.
Scores[d]에 저장하므로 query term이 바뀔 때 마다 다른 Scores 배열에 저장하게 된다.
잘 이해해보자 꽤나 어렵다.
정리
weight를 계산할 때 tf x idf로 계산했다. 그리고 weight를 기반으로 한 vector에 대해 cosine 유사도를 계산했다.
하지만 이런 방법 말고 옵션이 몇 가지 있다.

쿼리와 document에 다른 weighting을 쓰고싶다면 ddd.qqq와 같은 방식으로 나타낸다.
예를 들어 lnc.ltn은
- document에 대해 tf : log, df : no, normal : cosine
- query에 대해 tf : log, df : idf, normal : no
- 쿼리는 보통 normalization을 사용하지 않는다.
query : “best car insurance”
document : “car insurance auto insurance”
lnc.ltn을 계산해보자!

df는 문제에서 주어진다. N 또한 주어지는데 결과를 보면 N이 대략 10^6이다.
계산도 한 번 해보자. df, idf 빼고는 다 계산할 수 있다.