2024. 10. 2. 08:00ㆍCS/Information Retrieval
Tolerant retrieval
- 단어를 조금 다르게 써도 비슷한 단어를 검색해 주는 방식이다.
- 예를 들어 data의 철자를 잘못써서 dato로 써도 data를 옳게 찾아준다면 tolerant retrieval이다.
- exact match가 없을 경우 spelling correction 혹은 wildcard queries로 바꿔서 검색하는 방식이다.
- Tolerant retrieval을 구현하는 방법을 알아보자.
1. Dictionaries
용어부터 정의해 보자.
Term vocabulary는 일종의 데이터이다.
term vocalulary를 저장하는 자료 구조가 dictionary이다.
각 term은 document frequency, pointer to postings list 등의 정보와 함께 저장된다.
이 정보들을 fixed-length entry로 저장할 수 있고 array로 구현할 수 있다.

dictionary라 하면 바로 위의 그림을 떠올릴 수 있어야 한다.
dictionary는 term 뒤에 posting이 달려 있는 구조이므로 pointer를 포함해야 한다.
dictionary를 fixed-length array로 구현하면 낭비되는 공간도 많고 정해진 size 보다 더 큰 term이 들어오면 오류가 생긴다.
Data structures for looking up term
dictionary를 구현하는 주된 두 가지 자료구조는 hash, tree가 있다.
자료구조의 특성을 생각해 보면 해시는 검색의 속도가 O(1)로 상당히 빠르고 트리는 O(log n)이다.
term의 길이가 일정하면 hash를 사용해도 되는데 일정하지 않다면 hash를 사용할 수 없으므로 tree를 사용해야 한다.
자세히 알아보자.
Hashes
- query term을 해싱을 해서 value 값을 array entry에서 찾아서 바로 document list를 찾을 수 있다.
- tree 검색보다 hash 검색이 훨씬 빠르다.
- minor variants 한 단어는 찾을 수 없다. 예를 들어 resume, r´esum´e 이 두 단어를 전혀 다른 단어로 인식한다.
- 그 이유는 해싱 함수가 단어의 유사도와는 관계가 없고, 충돌이 나지 않게끔 분산하는 것에 집중하기 때문이다. 예시의 두 단어는 서로 멀리 떨어진 index로 해싱될 수 있고 그 경우 아주 사소한 변화지만 찾을 수 없다.
- prefix search, 즉 wild card를 사용한 검색 혹은 tolerant 검색이 힘들다.
- entry가 계속 새로 들어오면 주기적으로 해시 함수를 새로 만들어서 재해시 해야 한다.
- 해싱을 하게 되면 tolerant 검색은 힘들지만 속도는 빠르므로 잘 선택해야 한다.
Trees
- 어떤 글자로 시작하는 단어를 찾는 prefix search가 가능하다.
- 가장 간단한 트리는 이진트리인데 해시보다는 느리다.
- balanced tree를 사용하면 O(log N)으로 가능하다.
- Rebalancing tree도 O(log N)이 걸리므로 비싸다.

tri 구조에서는 path가 단어를 나타낸다. 트리의 노드 하나가 철자를 나타내는 것이다.
2. Wildcard queries
*를 포함한 term은 B-tree로 해결이 가능하다.
mon* 을 검색하면 mon으로 시작하는 단어를 길이도, 문자도 상관없이 찾는다.
B-tree dictionary를 사용하면 mon ≤ t < moo를 찾으면 돼서 간단하게 해결이 가능하다.
하지만 prefix가 아닌 *mon과 같은 postfix를 찾으려면 backwards, 단어를 뒤집어서 nom*에 대해 backwards B-tree를 만들어서 거기서 검색해야 한다.
그렇다면 *이 단어의 중간에 포함되는 경우는 어떻게 해결할까?
m*nchen에 대해 단어를 잘라서 m*, *nchen을 B-tree에서 찾아서 intersection을 하면 되지만 좀 비싸다.
permuterm index
그래서 나온 게 permuterm index이다. permuterm index는 * 가 어디에 나오던 딱 한 번의 B-tree search로 해결할 수 있다.
Basic idea는 wildcard query를 rotate 해서 prefix 형태로 만드는 것이다.
참고로 permutation은 순열이다. permuterm은 term의 permutation을 뜻한다.
HELLO에 대해 permutation을 구해보자.
permutation을 구하면 단어의 끝 철자를 구별할 수 없으므로 $를 붙여줘야 한다. 그럼 hello$, ello$h, llo$he, lo$hel, o$hell, and $hello 이렇게 6개의 permutation을 구할 수 있고 이를 permuterm이라 한다.
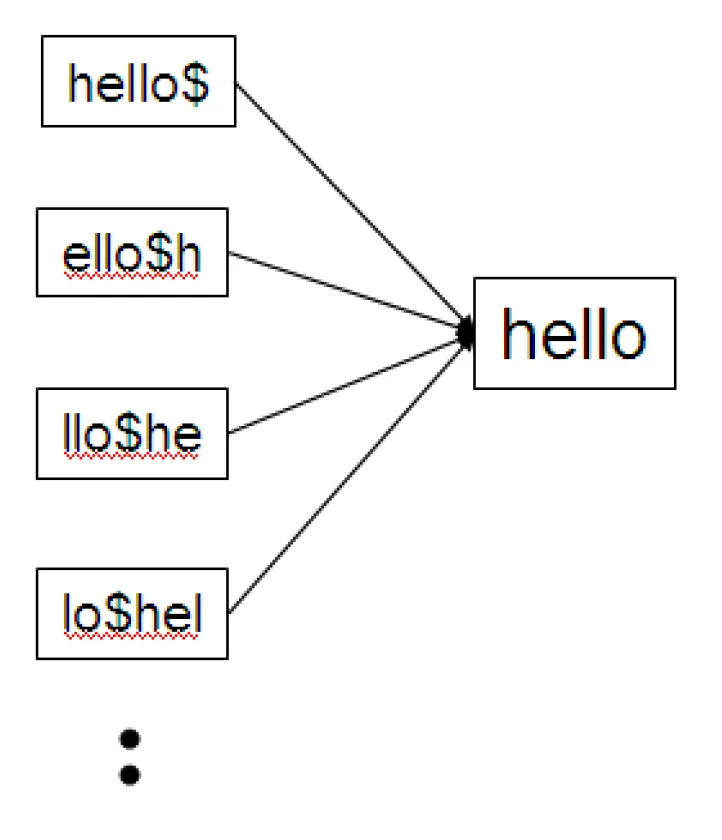
이렇게 만든 permuterm을 가지고 B-tree를 만들게 되면 B-tree size가 4~5배 커지긴 하지만 wildcard가 어디에 오던 가능하다.
트리를 여러 개 만들고 intersection을 해서 시간이 오래 걸리는 것보다 permuterm을 만들어서 메모리는 좀 많이 쓰더라도 빠르게 해결하는 것이 좋다.
예를 들어 생각해 보자.
- X를 검색하려면 X$를 보면 된다.
- X*를 검색하려면 rotation 한 $X*을 보면 된다. $X가 prefix이고 뒤에 *가 붙었으므로 B-tree에서 쉽게 찾을 수 있다.
- X* → X*$ → rotate 즉, permutation 중 *가 제일 뒤에 나오는 term을 찾으면 된다.
- *X를 검색하려면 X$*를 보면 된다.
- *X*를 검색하려면 *X*$의 permutation 중 X*$*를 검색하면 되는데, $는 단어로서의 역할은 하지 않으므로 X*를 검색하면 된다.
- X*Y는 X*Y$를 검색하면 되는데, rotate 시켜서 Y$X*를 검색하면 된다.
모든 케이스에 대해 직접 다 해보자!
permuterm index는 permuterm tree라고도 불리고 평균적으로 B tree가 4배 정도 커지게 된다.
k-gram indexes
permuterm index는 기존보다 4배 더 많은 메모리를 차지한다는 단점이 있었다. 그래서 메모리를 줄이려고 등장한 게 k-gram이다.
k-gram은 k개의 단어로 이루어진 sequence를 의미한다.
k-gram indexes는 k-gram을 가지고 inverted index를 만든 index이다.
2-gram은 bigram, 3-gram은 trigram이라 한다.
예를 들어 보자.
- from April is the cruelest month 여기서 bigram을 얻어보면, 다음과 같다. 단어의 앞뒤에 $를 추가해야 한다.
- $a ap pr ri il l$ $i is s$ $t th he e$ $c cr ru ue el le es st t$ $m mo on nt h$
기존에는 term을 가지고 document를 만들기 위해 inverted index를 만들었다. 이번에는 이렇게 만든 k-gram을 가지고 term을 찾기 위한 inverted index를 만들 수 있다.
3-gram으로 inverted index를 만들어보자. 왼쪽에는 k-gram word, 오른쪽에는 term list가 달리게 된다.

어떤 term을 찾고 싶으면 k-gram index에서 intersection을 구하면 된다.
k-gram을 가지고 mon*를 찾으려면 $m AND mo AND on 쿼리를 날리면 된다.
그런데 false positive 문제가 생긴다. MOON 결과 또한 나오는 것이다. MOON 또한 bigram을 모두 포함하기 때문이다.
그래서 original term mon*을 가지고 검색 이후에 filtering을 해줘야 한다. 모든 검색 결과를 mon*를 가지고 일치하는지 비교해야 하는 것이다.
다시 정리해 보자
- k-gram index는 공간 효율이 좋지만 postfiltering을 해야 한다.
- Permuterm은 공간 효율은 좋지 않지만 postfiltering을 요구하지 않는다.
3. Edit distance
타이핑 실수 등의 이유로 철자가 조금 틀려도 옳은 결과를 찾아주는 Tolerant retrieval을 위한 방법이 edit distance이다.
Edit distance는 edit operation을 몇 번 해서 옳은 결과를 나타낼 수 있는지이다. 두 단어 사이의 편집 거리라고 생각하면 된다.
편집이라 하면 insert, delete, replace가 기본적이고 swapping도 있을 수 있다.
Levenshtein distance
- edit distance의 일종이다.
- 편집의 기본 operation을 insert, delete, replace로 설정했다.
- 예시로 알아보자.
- dog - do : 1, insert
- cat - cart : 1, delete
- cat - cut : 1, replace
- cat - act : 2, delete and insert
- Damerau-Levenshtein distance는 swapping operation을 지원하므로 cat - act : 1이 된다.
- 타이핑할 때 철자가 앞뒤로 뒤바뀌는 경우가 많기 때문이다.
실제 계산을 한 번 해보자. cats, fast의 경우 최적의 minimum edit distance를 구하기는 쉽지 않다. 알고리즘은 다음과 같다.

dp based 알고리즘이다. m 배열이 dp 배열이라 생각하면 된다. 점화식을 설명하기 위해 아래 그림을 보자.
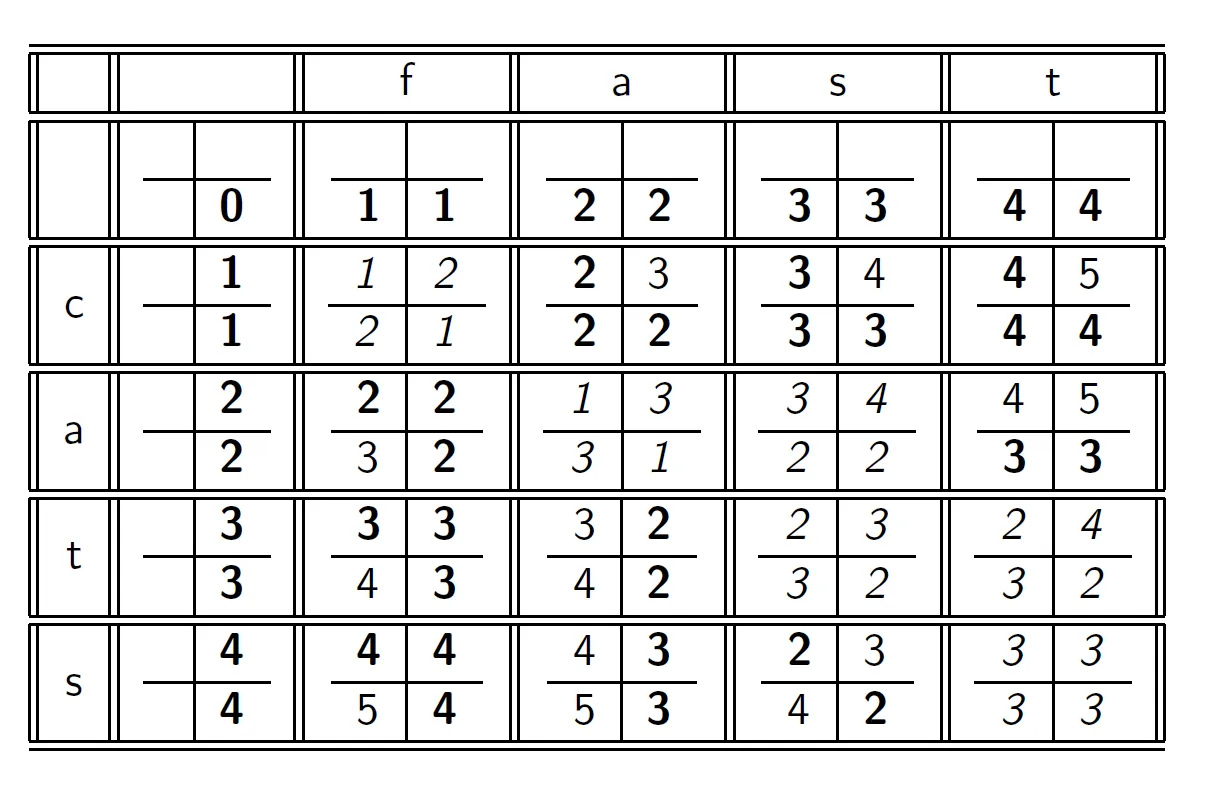
열에 target이 왔다고 생각해 두고 모든 연산은 행에서만 수행한다고 생각하면 편하다. target 단어를 첫 번째 단어, 행에 오는 단어를 두 번째 단어라 하고 차례대로 구해보자.
m [i, j]는 첫 번째 단어를 j 번째 글자까지, 두 번째 단어를 i 번째 글자까지 사용했을 때 edit distanc이다.
dp 문제는 항상 dp 정의, 점화식이 중요하다. 점화식을 구하기 위해 각 배열이 어떻게 계산되는지 생각해 보자.
0행 1열
- 첫 번째 단어가 null 이므로 c delete → 1
1행 0열
- 두 번째 단어가 null이므로 f insert → 1
1행 1열
- 0행 1열 + 1 → 0행 1열은 첫 번째 단어가 f, 두 번째 단어가 null인 상태에서 f, f로 맞춰주었다. 그 상태에서 1행 1열이 되면 두 번째 단어에 c가 추가되었으므로 두 번째 단어의 c delete
- 1행 0열 + 1 → 1행 0열은 첫 번째 단어가 null, 두 번째 단어가 c인 상태에서 c를 delete 해서 null, null로 맞춰주었다. 그 상태에서 1행 1열이 되면 첫 번째 단어에 f가 추가되므로 두 번째 단어에 f insert
- 0행 0열 + 1 → replace → f, f
이걸 일반화해 보면
m [i, j]이 될 수 있는 대상은 총 세 가지이다.
- m [i-1, j] + 1 → 두 번째 단어를 i - 1 번째 글자까지, 첫 번째 단어를 j까지 해서 맞춰두었는데 두 번째 단어 중 i 번째 글자가 들어왔으므로 i 번째 글자를 delete 하는 비용이다.
- m [i, j-1] + 1 → 첫 번째 단어를 j - 1 번째 글자까지, 첫 번째 단어를 i까지 해서 맞춰두었는데 첫 번째 단어 중 j 번째 글자가 들어왔으므로 j번째 글자를 두 번째 단어에 insert 하는 비용이다.
- m [i-1, j-1] → 첫 번째 단어의 j, 두 번째 단어의 i가 같은 경우
- m[i-1, j-1] + 1 → 첫 번째 단어의 j, 두 번째 단어의 i가 다른 경우 두 번째 단어의 i replace
이렇게 된다.
이 배열을 거꾸로 추적하여 왼쪽으로 가면 insert, 위로 가면 delete라 생각하고 최종 연산을 구할 수 있다.
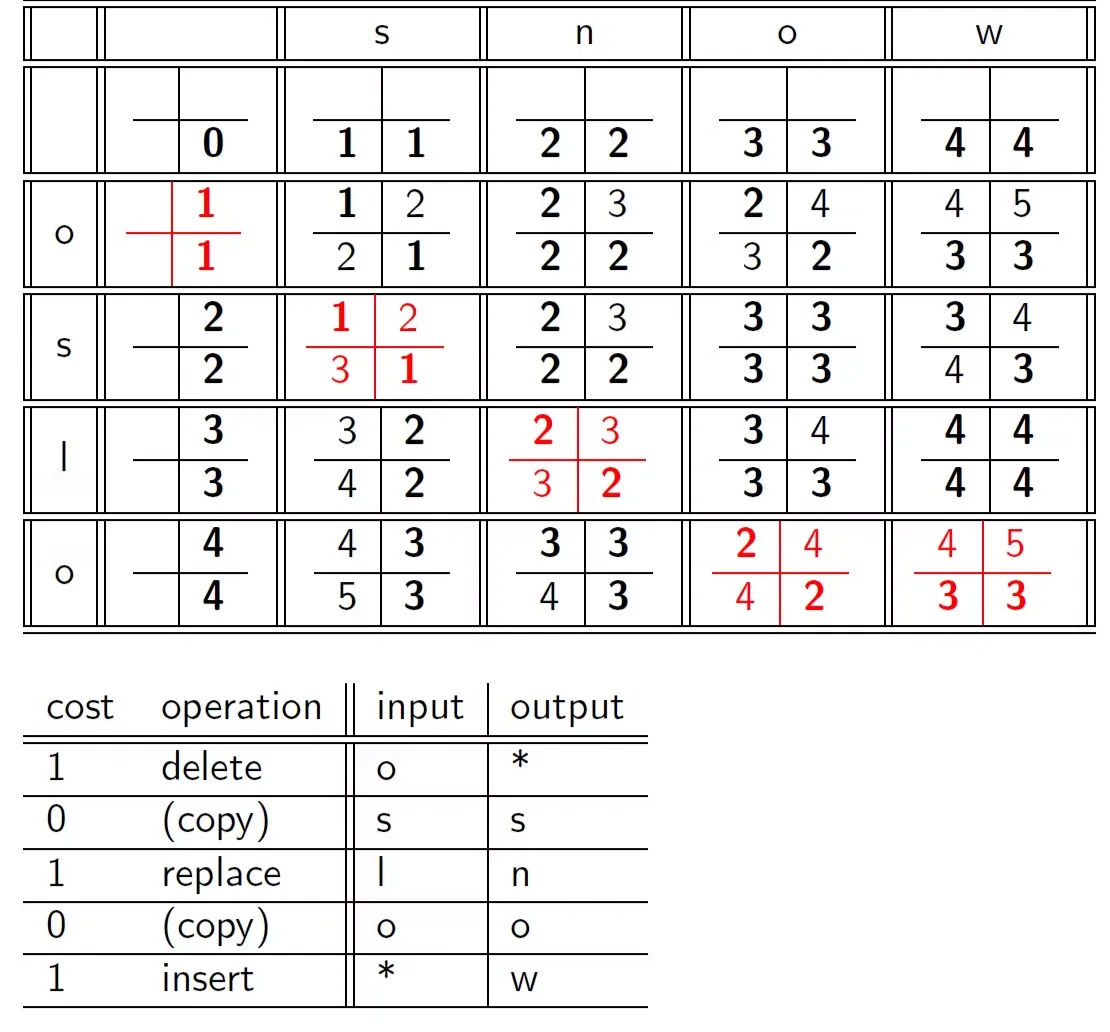
Weighted eidt distance
- 앞에서 구한 eidt distance는 모든 연산의 weights가 동일했다.
- 그러나 연산의 가중치는 관련된 문자에 따라 달라질 수 있다.
- 예를 들어 m은 n으로 잘못 입력될 가능성이 q로 잘못 입력될 가능성보다 더 높다. 따라서 m을 n으로 대체하는 편집 거리는 m을 q로 대체하는 편집 거리보다 더 적다.
- 따라서 입력으로 가중치 행렬이 필요하고 동적 프로그래밍을 가중치를 처리할 수 있도록 수정해야 한다.
edit distance는 주어진 쿼리에 대해 사전 설정된 편집 거리 내에 있는 모든 문자 시퀀스를 나열한다.
그리고 나열된 문자 시퀀스 집합을 사전에 정의된 올바른 단어 목록과 비교하여 교집합을 구한다.
교집합에서 사용자가 입력하려던 단어를 추정하여 추천함으로써 사용자가 잘못 입력한 단어나 오타를 교정할 수 있다.
4. Spelling correction
Will not catch typos resulting in correctly spelled words, e.g., an asteroid that fell form the sky
여기서 단어 form은 from의 오타이다. 그러나 실제 하는 단어이므로 문맥상 Isolated word를 찾아내야 하는데 굉장히 어려운 일이다.
5. Soundex
데이터, 데이타와 같이 소리 나는 대로 같은 말이지만 정보 검색에서는 전혀 다른 단어가 존재한다.
그래서 소리를 기반으로 matching 하는 알고리즘이 필요하고 이를 Soundex라 한다. 알고리즘을 알아보자.
- 단어의 첫 글자는 유지한다.
- A, E, I, O, U, H, W, Y는 0으로 바꾼다. 모음이거나 모음 유사한 발음을 0으로 바꾸는 것이다.
- 다음 글자를 숫자로 바꾼다.
- B, F, P, V → 1
- C, G, J, K, Q, S, X, Z → 2
- D, T → 3
- L → 4
- M, N → 5
- R → 6
- 연속해서 나오는 똑같은 숫자는 pair가 나올 때마다 하나씩 줄인다. 세 개가 나오면 두 개가 되는 것이다.
- 결과에서 모든 0을 지운다. 앞에서부터 4글자를 넘겨준다. 이때 칸이 모자라면 끝을 0으로 채워준다.
HERMAN으로 직접 해보자.
- Retain H
- ERMAN → 0 RM0 N
- 0RM0N → 06505
- 06505 → 06505 (반복되는 숫자가 없음)
- 06505 → 655 (0 제거)
- Return H655
- HERMAN의 Soundex Code는 H655가 된다.
결과를 보면 HERMANN과 HERMAN의 Soundex Code는 같아진다.
정보 검색에서 유용하지는 않지만 high recall을 요구하는 task, 즉 결과에 오답이 많이 포함되더라도 정답을 최대한 많이 뽑아내는 task에서 많이 사용한다.
참고로 Precision은 Recall과 반대되는 개념으로 정답률이 높아야 좋은 평가 지표이다.