2024. 9. 30. 16:49ㆍCS/Information Retrieval
1. Introduction
Information Retrieval
- 데이터베이스에서 처리하는 정형화된 데이터가 아닌 텍스트 같은 비정형 데이터로 이루어진 문서와 같은 물질을 찾는 것이다.
- 문장을 파악하는 것인데, 예를 들어 홍길동은 A+를 받았다.라는 문장을 보고 홍길동 : A+라고 파악하는 것을 말한다.
- 사용자가 찾고자 하는(information need) 비정형 데이터를 검색하는 것이다.
- 예를 들어 사용자가 파리 지도라고 검색한다면 초파리의 염색 지도가 나올 수 있다. 그러나 사용자가 원하는 건 프랑스 파리의 지도이다.
- 이러한 정보를 대용량 문서에서 찾아주는 것이 정보 검색이다.
- 즉, 핵심은 정보 검색은 unstructured를 갖는 text를 documents에서 찾는 것인데, 큰 collection에서 information need를 만족하면서 찾아야 한다는 것이다.
Boolean Retrieval
- 단어가 맞는지 아닌지 boolean 값으로만 판단한다. 가장 간단한 검색 모델이다.
- 예를 들어 생각해보자. CASEAR AND BRUTUS를 검색하면 AND를 써서 일치하는걸 모두 리턴한다. 즉 [w1 w2 … wn]을 쿼리로 검색하면 AND 사이사이에 삽입한다. w1 AND w2 AND … AND wn 이런 식이다.
Boolean Retrieval의 문제는 다음과 같다.
- 예를 들어 데이터를 검색했는데 데이타는 데이터 와 같은 의미를 가지지만 검색 결과에는 포함되지 않는다.
- 질문이 길면 문제가 생긴다. 답이 너무 짧을 수 있다.
- 매칭된 결과를 순서 없이, 중요도 없이 다 보여주거나 너무 복잡한 쿼리에 대한 것은 대답을 내놓을 수 없다.
- Boolean Retrieval은 Ranking을 사용하지 않는다.
그래서 도입된 게 Ranking of result set이다. Ranking은 확률이라고 생각하면 된다.
simple boolean은 검색된 문서의 처음부터 끝까지 필요한 게 뭔지 다 봐야 하지만 Ranking of the result set은 유사도가 높은 게 먼저 나오므로 다 볼 필요가 없을 수 있다.
2. Inverted index
셰익스피어가 쓴 희곡 중에서 주인공을 찾아내는 검색을 한다고 생각해 보자.
예를 들어 BRUTUS AND CAESAR, but NOT CALPURNIA를 검색했다. grep을 가지고 BRUTUS, CAESAR를 검색해서 나온 결과를 AND를 한다. 그리고 결과에서 CALPURNIA가 들어가는걸 빼면 된다.
위의 방식처럼 boolean 처리를 grep 을 가지고 할 수 있지만, 굉장히 느리고 결과가 파일 단위가 아닌, line 단위로 출력된다는 문제가 있다. not 연산도 하기 힘들다.
아무튼 and, not 연산을 grep으로 구현할 수 있다.
그런데 만약 near 명령어, 예를 들어 ROMANS near COUNTRYMAN이라는 명령어는 불가능하다. 해당 명령은 ROMANS 근처(한 두 단어 떨어짐) COUNTRYMAN을 검색하는 건 grep으로는 불가능하다.
Term-document incidence matrix

각 행은 주인공, 즉 찾으려는 term 용어를 나타낸다. 각 열은 희극의 제목, 즉 document를 나타낸다. 1은 나타나는 것이고 0은 나타나지 않는 것이다. boolean 이기에 나타나기만 하면 1이고 많이 나타나도 1이다.
위의 표를 term document incidence matrix라 한다. Term이 왼쪽에 있고 위쪽에 document가 있는 matrix이다! Term document incidence matrix라 하면 바로 위의 그림을 떠올릴 수 있도록 익혀두자!
Incidence vectors
term document incidence matrix를 가지고 만든 벡터이다. term을 기준으로 불린 값을 나열한 벡터이고 term vector라고도 한다.
위의 표를 예로 들면 ANTHONY 벡터는 (1, 1, 0, 0, 0, 1)이다. CALPURINA의 벡터는 (0, 1, 0, 0, 0, 0)이다.
term vector를 가지고 불린 연산을 수행할 수 있다. BRUTUS CAESAR NOT CALPURINA를 검색한다면
110100 AND 110111 AND 101111(원래 CALPURINA는 010000)
⇒ 100100이 된다.
Inverted Index
이제 문제는 document가 커질 때가 된다. 예를 들어 10^6개의 문서에 대해 각 문서가 토큰(여기서는 단어)이 10^3개 존재한다면 전체 토큰은 10^9개가 된다.
10억, 즉 1G개의 토큰이 있고 한 토큰당 6byte의 길이를 가진다면 총 6 GB의 메모리를 차지하게 된다. 그 collection 중 고유한 단어의 종류가 50만 개 (M = 50만) 이라 하자.
이를 가지고 term document incidence matrix를 만들다면 term이 50만개 document가 100만 개다. 그럼 matrix의 크기는 50만 * 100만 = half trillion이 된다. 0.5 T = 500G이다.
참고 ) 수의 표현을 잘 알아두자.
10^3 : K, 천, thousands
10^6 : M, 백만, million
10^9 : G, 십업, billion
10^12 : T, 조, trillion
matrix를 메모리에 올려보면 500G bit , 대략 60GB로 너무 크다.
또 matrix를 보면 대부분이 0이고 1이 조금만 있다, sparse 하다. 따라서 matrix를 그냥 올리면 너무 비효율적이고 linked list로 1인 것만 표현할 수 있다. 그럼 메모리를 훨씬 줄여서 콤팩트하게 표현할 수 있다.
matrix를 linked list로 바꾸면 단어를 중심으로 postings (문서 번호의 집합) 이 달려있게 된다. 이 linked list로 나타낸 구조를 Inverted Index 라 한다. 굉장히 중요한 정보 검색의 기본 구조이다.

Inverted Index의 기본 구조는 왼쪽에 term, dictionary가 있고 오른쪽에 postings, 문서 번호의 집합이 존재한다. Inverted Index를 생각하면 바로 위의 구조가 떠올라야 한다!
[Friends, Romans, countrymen. …], [So let it be with Caesar …] 이렇게 두 개의 문서에 대해 어떻게 inverted index를 만들 수 있을까?
- 각 문서를 토큰화해야 한다. Friends, Romans, countrymen, So, …
- 띄어쓰기 단위로 자르고 대문자, 복수형을 정규화시킨다. 그럼 term의 수가 줄어들게 된다. 형태소 분석이라고도 한다. → friend, roman, countryman, so, …

이제 inverted index를 구현하면 된다.
1. 1번 문서에 나오는 단어를 다 찍으면서 document ID를 달아준다.

2. 단어를 중심으로 postings를 sorting 하고 하나의 list로 합친다.

3. postings list를 만들고 document frequency를 결정한다.

이 과정을 직접 어떻게 해야 하는지 시뮬레이션해보자! 여기서 말하는 빈도는 한 document에서 몇 번 나왔는지가 아니라 몇 개의 document에서 나왔는지이다.
결과를 딕셔너리와 posting file로 만들면 된다.

inverted index로 matrix가 너무 크다는 문제를 해결할 수 있었다. matrix를 inverted index로 만들었을 때 크기가 얼마나 줄어드는지, 어떻게 처리할 건지를 고민해봐야 한다. document가 너무 많다면 index를 compress 하는 것도 생각해봐야 하고 모든 걸 검색하지 말고 쿼리에 매칭될 가능성이 높은걸 ranking 해서 검색한다던지 등을 배워야 한다.
3. Processsing Boolean queries
term docuemnt incidence matrix는 term에 대해서 벡터를 뽑아서 AND 연산을 수행하면 된다. 하지만 inverted index에서는 쉽지 않다. bit operation으로 하려니까 bit가 너무 많이 든다. 따라서 다른 로직을 가지고 검색해야 한다.
- BRUTUS AND CALPURNIA에 대해 각 단어에 대한 postings file을 뽑아낸다.
- 교집합(intersection)을 구한다. 자세한 방법은 예시로 살펴보자.
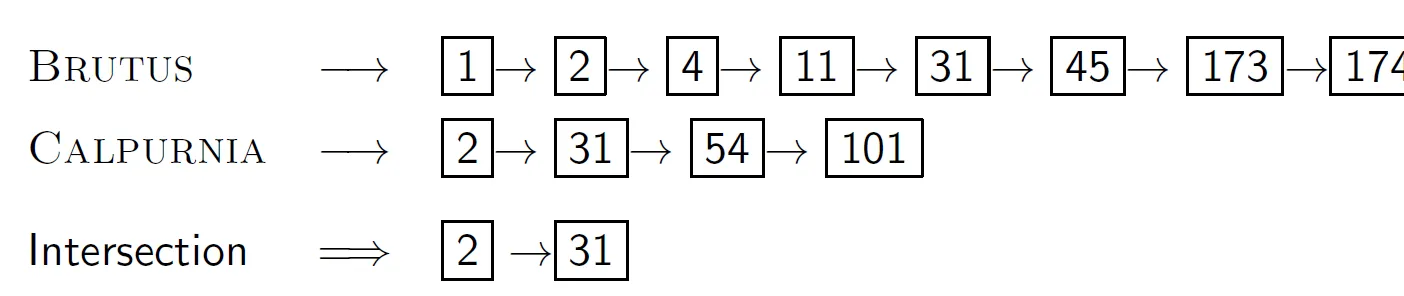
1, 2를 비교하고 다르므로 작은 쪽 1을 증가시킨다. 2, 2 같으므로 둘 다 증가시킨다. 4 31 다르므로 작은쪽 4를 증가시킨다. 핵심은 작은 쪽을 증가시킨다는 것이다. 시간 복잡도가 n 길이에 대해 O(n)이다. 굉장히 효과적이다. 그러나 전제는 posting file이 sort 되어있어야 한다는 점이다.
이 알고리즘을 꼭 표현할 수 있어야 한다. 직접 짜보자!

다른 예시도 보자.

OR에 대해서는 다르면 작은 걸 하나 넣고 하나 증가, 같으면 둘 중 하나만 넣으면 된다. 이것도 알고리즘으로 짜보자.
NOT은 inverse posting file을 만들어서 없는 걸 넣는 방법도 있고 결과에서 빼는 방법도 있다. 이것도 해보자.
이제 AND OR NOT에 대해 대답할 수 있다. Boolean retrieval에서는 문서를 term 들의 집합으로 보는 것이다. 법률 쪽, 이메일 검색 등에서는 아직도 사용되고 있다.
Weatlaw라는 법률 검색 시스템에서 과거부터 계속 boolean search를 사용하고 있다. westlaw는 근접한 단어를 찾는 방법으로 /3, /s, /p을 도입했다.
법률 정보는 보다 작고 우선순위가 없이 원하는 법률을 모두 찾아야 하므로 불린으로도 괜찮다.
4. Query optimization
쿼리를 어떻게 처리하느냐에 따라 성능이 크게 차리난다.
쿼리가 3 이상의 terms에 대해 AND로 들어온 경우를 생각해 보자. 각 텀에 대해 postings list를 얻고 AND 연산을 취해줘야 한다. 예를 들어 BRUTUS AND CALPURINA AND CAESAR 쿼리를 처리하는 가장 좋은 방법은 뭘까?
가장 간단하고 효과적인 방법은 frequency가 증가하는 순서로 처리하는 것이다. postings list가 가장 짧은 term에서 시작하는 것이다.
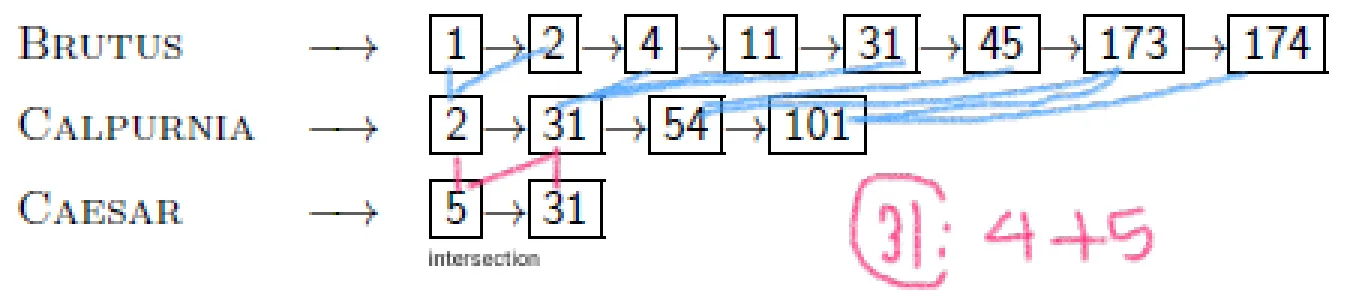
위의 알고리즘 코드는 다음과 같다.

AND 연산 외에 일반적인 연산에 대해 쿼리 최적화를 해보자.
(MADDING OR CROWD) AND (IGNOBLE OR STRIFE)
위의 쿼리는 OR 후 AND 연산을 해야 한다. 일단 모든 term의 frequency를 얻고 OR도 AND와 똑같이 frequency가 작은 것부터 연산하는 게 좋다.